Нейронные сети, перцептрон

Материал из Викиконспекты
Версия от 19:32, 4 сентября 2022; Maintenance script (обсуждение | вклад) (rollbackEdits.php mass rollback)
(разн.) ← Предыдущая | Текущая версия (разн.) | Следующая → (разн.)
Перейти к: навигация, поиск

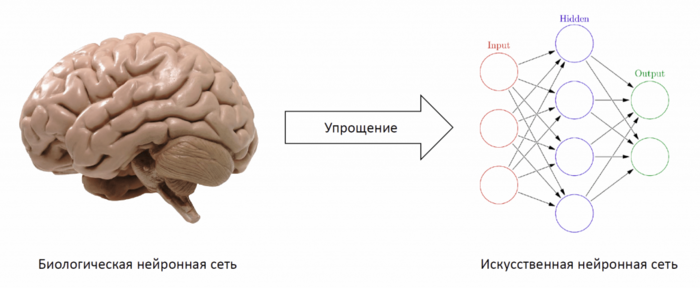
Искусственная нейронная сеть (ИНС) (англ. Artificial neural network (ANN)) — упрощенная модель биологической нейронной сети, представляющая собой совокупность искусственных нейронов, взаимодействующих между собой.

Рисунок 1. Упрощение биологической нейронной сети

Основные принципы работы нейронных сетей были описаны еще в 1943 году Уорреном Мак-Каллоком и Уолтером Питтсом[1]. В 1957 году нейрофизиолог Фрэнк Розенблатт разработал первую нейронную сеть[2], а в 2010 году большие объемы данных для обучения открыли возможность использовать нейронные сети для машинного обучения.

На данный момент нейронные сети используются в многочисленных областях машинного обучения и решают проблемы различной сложности.

Структура нейронной сети

Рисунок 2. Схема искусственного нейрона

Хорошим примером биологической нейронной сети является человеческий мозг. Наш мозг — сложнейшая биологическая нейронная сеть, которая принимает информацию от органов чувств и каким-то образом ее обрабатывает (узнавание лиц, возникновение ощущений и т.д.). Мозг же, в свою очередь, состоит из нейронов, взаимодействующих между собой.

Для построения искусственной нейронной сети будем использовать ту же структуру. Как и биологическая нейронная сеть, искусственная состоит из нейронов, взаимодействующих между собой, однако представляет собой упрощенную модель. Так, например, искусственный нейрон, из которых состоит ИНС, имеет намного более простую структуру: у него есть несколько входов, на которых он принимает различные сигналы, преобразует их и передает другим нейронам. Другими словами, искусственный нейрон — это такая функция [math]\mathbb{R}^n \rightarrow \mathbb{R}[/math], которая преобразует несколько входных параметров в один выходной.

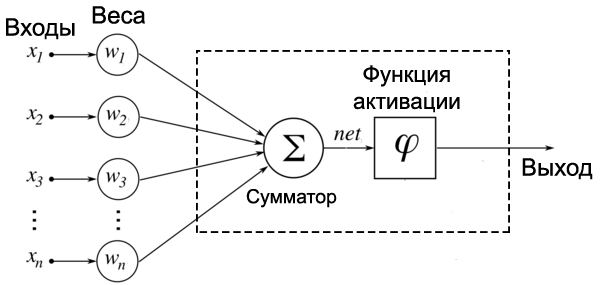
Как видно на рисунке справа, у нейрона есть [math]n[/math] входов [math]x_i[/math], у каждого из которого есть вес [math]w_i[/math], на который умножается сигнал, проходящий по связи. После этого взвешенные сигналы [math]x_i \cdot w_i[/math] направляются в сумматор, который аггрегирует все сигналы во взвешенную сумму. Эту сумму также называют [math]net[/math]. Таким образом, [math]net = \sum_{i=1}^{i=n} w_i \cdot x_i = w^T \cdot x[/math].

Просто так передавать взвешенную сумму [math]net[/math] на выход достаточно бессмысленно — нейрон должен ее как-то обработать и сформировать адекватный выходной сигнал. Для этих целей используют функцию активации, которая преобразует взвешенную сумму в какое-то число, которое и будет являться выходом нейрона. Функция активации обозначается [math]\phi(net)[/math]. Таким образом, выходов искусственного нейрона является [math]\phi(net)[/math].

Для разных типов нейронов используют самые разные функции активации, но одними из самых популярных являются:

  • Функция единичного скачка. Если [math]net \gt threshold[/math], [math]\phi(net) = 1[/math], а иначе [math]0[/math];
  • Сигмоидальная функция. [math]\phi(net) = \frac{1}{1 + exp(-a \cdot net)}[/math], где параметр [math]a[/math] характеризует степень крутизны функции;
  • Гиперболический тангенс. [math]\phi(net) = tanh(\frac{net}{a})[/math], где параметр [math]a[/math] также определяет степень крутизны графика функции;
  • Rectified linear units (ReLU). [math]ReLU(x) = \begin{cases} x & x \geq 0 \\ 0 & x \lt 0 \end{cases} = \max(x, 0)[/math].

Виды нейронных сетей

Разобравшись с тем, как устроен нейрон в нейронной сети, осталось понять, как их в этой сети располагать и соединять.

Как правило, в большинстве нейронных сетей есть так называемый входной слой, который выполняет только одну задачу — распределение входных сигналов остальным нейронам. Нейроны этого слоя не производят никаких вычислений. В остальном нейронные сети делятся на основные категории, представленные ниже.

Однослойные нейронные сети

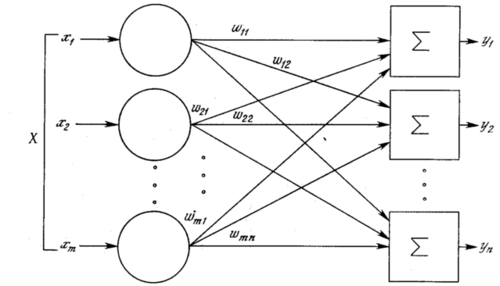
Рисунок 3. Схема однослойной нейронной сети

Однослойная нейронная сеть (англ. Single-layer neural network) — сеть, в которой сигналы от входного слоя сразу подаются на выходной слой, который и преобразует сигнал и сразу же выдает ответ.

Как видно из схемы однослойной нейронной сети, представленной справа, сигналы [math]x_1, x_2, \ldots x_n[/math] поступают на входной слой (который не считается за слой нейронной сети), а затем сигналы распределяются на выходной слой обычных нейронов. На каждом ребре от нейрона входного слоя к нейрону выходного слоя написано число — вес соответствующей связи.








Многослойные нейронные сети

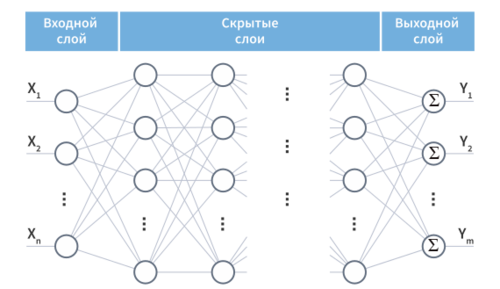
Рисунок 4. Схема многослойной нейронной сети

Многослойная нейронная сеть (англ. Multilayer neural network) — нейронная сеть, состоящая из входного, выходного и расположенного(ых) между ними одного (нескольких) скрытых слоев нейронов.

Помимо входного и выходного слоев эти нейронные сети содержат промежуточные, скрытые слои. Такие сети обладают гораздо большими возможностями, чем однослойные нейронные сети, однако методы обучения нейронов скрытого слоя были разработаны относительно недавно.

Работу скрытых слоев нейронов можно сравнить с работой большого завода. Продукт (выходной сигнал) на заводе собирается по стадиям на станках. После каждого станка получается какой-то промежуточный результат. Скрытые слои тоже преобразуют входные сигналы в некоторые промежуточные результаты.


Сети прямого распространения

Сети прямого распространения (англ. Feedforward neural network) (feedforward сети) — искусственные нейронные сети, в которых сигнал распространяется строго от входного слоя к выходному. В обратном направлении сигнал не распространяется.

Все сети, описанные выше, являлись сетями прямого распространения, как следует из определения. Такие сети широко используются и вполне успешно решают определенный класс задач: прогнозирование, кластеризация и распознавание.

Однако сигнал в нейронных сетях может идти и в обратную сторону.

Сети с обратными связями

Рисунок 5. Схема сети с обратными связями

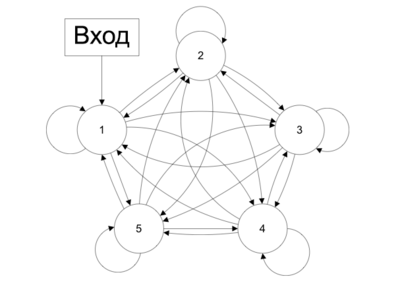
Сети с обратными связями (англ. Recurrent neural network) — искусственные нейронные сети, в которых выход нейрона может вновь подаваться на его вход. В более общем случае это означает возможность распространения сигнала от выходов к входам.

В сетях прямого распространения выход сети определяется входным сигналом и весовыми коэффициентами при искусственных нейронах. В сетях с обратными связями выходы нейронов могут возвращаться на входы. Это означает, что выход какого-нибудь нейрона определяется не только его весами и входным сигналом, но еще и предыдущими выходами (так как они снова вернулись на входы).

Обучение нейронной сети

Обучение нейронной сети — поиск такого набора весовых коэффициентов, при котором входной сигнал после прохода по сети преобразуется в нужный нам выходной.

Это определение «обучения нейронной сети» соответствует и биологическим нейросетям. Наш мозг состоит из огромного количества связанных друг с другом нейросетей, каждая из которых в отдельности состоит из нейронов одного типа (с одинаковой функцией активации). Наш мозг обучается благодаря изменению синапсов — элементов, которые усиливают или ослабляют входной сигнал.

Если обучать сеть, используя только один входной сигнал, то сеть просто «запомнит правильный ответ», а как только мы подадим немного измененный сигнал, вместо правильного ответа получим бессмыслицу. Мы ждем от сети способности обобщать какие-то признаки и решать задачу на различных входных данных. Именно с этой целью и создаются обучающие выборки.

Обучающая выборка — конечный набор входных сигналов (иногда вместе с правильными выходными сигналами), по которым происходит обучение сети.

После обучения сети, то есть когда сеть выдает корректные результаты для всех входных сигналов из обучающей выборки, ее можно использовать на практике. Однако прежде чем сразу использовать нейронную сеть, обычно производят оценку качества ее работы на так называемой тестовой выборке.

Тестовая выборка — конечный набор входных сигналов (иногда вместе с правильными выходными сигналами), по которым происходит оценка качества работы сети.

Само обучение нейронной сети можно разделить на два подхода: обучение с учителем[на 28.01.19 не создан] и обучение без учителя[на 28.01.19 не создан]. В первом случае веса меняются так, чтобы ответы сети минимально отличались от уже готовых правильных ответов, а во втором случае сеть самостоятельно классифицирует входные сигналы.

Перцептрон

Рисунок 6. Схема перцептрона

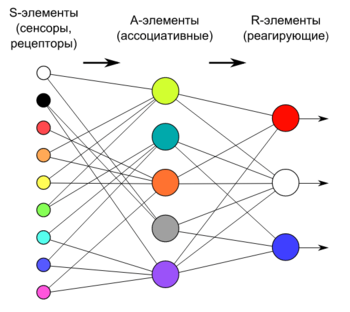
Перцептрон (англ. Perceptron) — простейший вид нейронных сетей. В основе лежит математическая модель восприятия информации мозгом, состоящая из сенсоров, ассоциативных и реагирующих элементов.

История

Идею перцептрона предложил нейрофизиолог Фрэнк Розенблатт. Он предложил схему устройства, моделирующего процесс человеческого восприятия, и назвал его «перцептроном» (от латинского perceptio — восприятие). В 1960 году Розенблатт представил первый нейрокомпьютер — «Марк-1», который был способен распознавать некоторые буквы английского алфавита.

Таким образом перцептрон является одной из первых моделей нейросетей, а «Марк-1» — первым в мире нейрокомпьютером.

Описание

В основе перцептрона лежит математическая модель восприятия информации мозгом. Разные исследователи по-разному его определяют. В самом общем своем виде (как его описывал Розенблатт) он представляет систему из элементов трех разных типов: сенсоров, ассоциативных элементов и реагирующих элементов.

Принцип работы перцептрона следующий:

  1. Первыми в работу включаются S-элементы. Они могут находиться либо в состоянии покоя (сигнал равен 0), либо в состоянии возбуждения (сигнал равен 1);
  2. Далее сигналы от S-элементов передаются A-элементам по так называемым S-A связям. Эти связи могут иметь веса, равные только -1, 0 или 1;
  3. Затем сигналы от сенсорных элементов, прошедших по S-A связям, попадают в A-элементы, которые еще называют ассоциативными элементами;
    • Одному A-элементу может соответствовать несколько S-элементов;
    • Если сигналы, поступившие на A-элемент, в совокупности превышают некоторый его порог ​[math]\theta[/math]​, то этот A-элемент возбуждается и выдает сигнал, равный 1;
    • В противном случае (сигнал от S-элементов не превысил порога A-элемента), генерируется нулевой сигнал;
  4. Далее сигналы, которые произвели возбужденные A-элементы, направляются к сумматору (R-элемент), действие которого нам уже известно. Однако, чтобы добраться до R-элемента, они проходят по A-R связям, у которых тоже есть веса (которые уже могут принимать любые значения, в отличие от S-A связей);
  5. R-элемент складывает друг с другом взвешенные сигналы от A-элементов, а затем
    • если превышен определенный порог, генерирует выходной сигнал, равный 1;
    • eсли порог не превышен, то выход перцептрона равен -1.

Для элементов перцептрона используют следующие названия:

  • S-элементы называют сенсорами;
  • A-элементы называют ассоциативными;
  • R-элементы называют реагирующими.

Классификация перцептронов

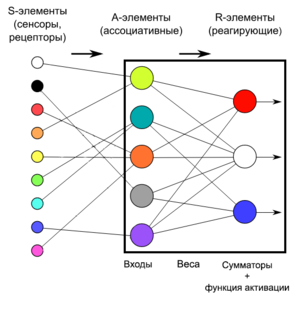
Рисунок 7. Схема однослойного перцептрона

Перцептрон с одним скрытым слоем (элементарный перцептрон, англ. elementary perceptron) — перцептрон, у которого имеется только по одному слою S, A и R элементов.

Однослойный персептрон (англ. Single-layer perceptron) — перцептрон, каждый S-элемент которого однозначно соответствует одному А-элементу, S-A связи всегда имеют вес 1, а порог любого А-элемента равен 1. Часть однослойного персептрона соответствует модели искусственного нейрона.

Его ключевая особенность состоит в том, что каждый S-элемент однозначно соответствует одному A-элементу, все S-A связи имеют вес, равный +1, а порог A элементов равен 1. Часть однослойного перцептрона, не содержащая входы, соответствует искусственному нейрону, как показано на картинке. Таким образом, однослойный перцептрон — это искусственный нейрон, который на вход принимает только 0 и 1.

Однослойный персептрон также может быть и элементарным персептроном, у которого только по одному слою S,A,R-элементов.

Многослойный перцептрон по Розенблатту (англ. Rosenblatt multilayer perceptron) — перцептрон, который содержит более 1 слоя А-элементов.

Многослойный перцептрон по Румельхарту (англ. Rumelhart multilater perceptron) — частный случай многослойного персептрона по Розенблатту, с двумя особенностями:

  • S-A связи могут иметь произвольные веса и обучаться наравне с A-R связями;
  • Обучение производится по специальному алгоритму, который называется обучением по методу обратного распространения ошибки.

Обучение перцептрона

Задача обучения перцептрона — подобрать такие [math]w_0, w_1, w_2, \ldots, w_n[/math], чтобы [math]sign(\sigma(w_0 + w_1 \cdot x_1 + w_2 \cdot x_2 + \ldots + w_n \cdot x_n))[/math] как можно чаще совпадал с [math]y(x)[/math] — значением в обучающей выборке (здесь [math]\sigma[/math] — функция активации). Для удобства, чтобы не тащить за собой свободный член [math]w_0[/math], добавим в вектор $x$ лишнюю «виртуальную размерность» и будем считать, что [math]x = (1, x_1, x_2, \ldots, x_n)[/math]. Тогда [math]w_0 + w_1 \cdot x_1 + w_2 \cdot x_2 + \ldots + w_n \cdot x_n[/math] можно заменить на [math]w^T \cdot x[/math].

Чтобы обучать эту функцию, сначала надо выбрать функцию ошибки, которую потом можно оптимизировать градиентным спуском. Число неверно классифицированных примеров не подходит на эту кандидатуру, потому что эта функция кусочно-гладкая, с массой разрывов: она будет принимать только целые значения и резко меняться при переходе от одного числа неверно классифицированных примеров к другому. Поэтому использовать будем другую функцию, так называемый критерий перцептрона: [math]E_P(w) = -\sum_{x \in M} y(x)(\sigma(w^T \cdot x))[/math], где [math]M[/math] — множество примеров, которые перцептрон с весами [math]w[/math] классифицирует неправильно.

Иначе говоря, мы минимизируем суммарное отклонение наших ответов от правильных, но только в неправильную сторону; верный ответ ничего не вносит в функцию ошибки. Умножение на [math]y(x)[/math] здесь нужно для того, чтобы знак произведения всегда получался отрицательным: если правильный ответ −1, значит, перцептрон выдал положительное число (иначе бы ответ был верным), и наоборот. В результате у нас получилась кусочно-линейная функция, дифференцируемая почти везде, а этого вполне достаточно.

Теперь [math]E_P(w)[/math] можно оптимизировать градиентным спуском. На очередном шаге получаем: [math]w^{(\tau+1)} = w^{(\tau)} − \eta\triangledown_w E_P(w)[/math].

Алгоритм такой — мы последовательно проходим примеры [math]x_1, x_2, \ldots[/math] из обучающего множества, и для каждого [math]x_n[/math]:

  • если он классифицирован правильно, не меняем ничего;
  • а если неправильно, прибавляем [math]\eta \triangledown_w E_P(w)[/math].

Ошибка на примере [math]x_n[/math] при этом, очевидно, уменьшается, но, конечно, совершенно никто не гарантирует, что вместе с тем не увеличится ошибка от других примеров. Это правило обновления весов так и называется — правило обучения перцептрона, и это было основной математической идеей работы Розенблатта.

Применение

  • Решение задач классификации, если объекты классификации обладают свойством линейной разделимости;
  • Прогнозирование и распознавание образов;
  • Управление агентами[3].

Примеры кода

Пример использования с помощью scikit-learn[4]

Будем классифицировать с помощью перцептрона датасет MNIST[5]. 

 # Load required libraries
 from sklearn import datasets
 from sklearn.preprocessing import StandardScaler
 from sklearn.linear_model import Perceptron      #Single-layer perceptron
 from sklearn.neural_network import MLPClassifier #Multilayer perceptron 
 from sklearn.model_selection import train_test_split
 from sklearn.metrics import accuracy_score
 import numpy as np

 # Load the mnist dataset
 mnist = datasets.load_digits()

 # Create our X and y data
 n_samples = len(mnist.images)
 X = mnist.images.reshape((n_samples, -1))
 y = mnist.target

 # Split the data into 70% training data and 30% test data
 X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)

 # Train the scaler, which standarizes all the features to have mean=0 and unit variance
 sc = StandardScaler()
 sc.fit(X_train)

 # Apply the scaler to the X training data
 X_train_std = sc.transform(X_train)

 # Apply the SAME scaler to the X test data
 X_test_std = sc.transform(X_test)

 # Create a single-layer perceptron object with the parameters: 40 iterations (epochs) over the data, and a learning rate of 0.1
 ppn = Perceptron(n_iter=40, eta0=0.1, random_state=0)
 # Create a multilayer perceptron object
 mppn = MLPClassifier(solver='lbfgs', alpha=1e-5, hidden_layer_sizes=(256, 512, 128), random_state=1)

 # Train the perceptrons
 ppn.fit(X_train_std, y_train)
 mppn.fit(X_train_std, y_train)

 # Apply the trained perceptrons on the X data to make predicts for the y test data
 y_pred = ppn.predict(X_test_std)
 multi_y_pred = mppn.predict(X_test_std)

 # View the accuracies of the model, which is: 1 - (observations predicted wrong / total observations)
 print('Single-layer perceptron accuracy: %.4f' % accuracy_score(y_test, y_pred))
 print('Multilayer perceptron accuracy: %.4f' % accuracy_score(y_test, multi_y_pred))

Вывод: 

 Single-layer perceptron accuracy: 0.9574
 Multilayer perceptron accuracy: 0.9759

Пример использования с помощью tensorflow[6]

Будем классифицировать цифры из того же датасета MNIST. 

 # Load required libraries
 import tensorflow as tf
 from tensorflow.examples.tutorials.mnist import input_data

 #Load MNIST dataset
 mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)

 #placeholder for test data
 x = tf.placeholder(tf.float32, [None, 784])
 #placeholder for weights and bias
 W = tf.Variable(tf.zeros([784, 10]))
 b = tf.Variable(tf.zeros([10]))
 #tensorflow model
 y = tf.nn.softmax(tf.matmul(x, W) + b)
 
 #loss function
 y_ = tf.placeholder(tf.float32, [None, 10])
 cross_entropy = tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(y), reduction_indices=[1]))

 #gradient descent step
 train_step = tf.train.GradientDescentOptimizer(0.5).minimize(cross_entropy)

 init = tf.initialize_all_variables()
 sess = tf.Session()
 sess.run(init)
 for i in range(1000):
   batch_xs, batch_ys = mnist.train.next_batch(100)
   sess.run(train_step, feed_dict={x: batch_xs, y_: batch_ys})
 correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1))
 accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
 print("Accuracy: %s" % sess.run(accuracy, feed_dict={x: mnist.test.images, y_: mnist.test.labels}))
Рисунок 8.
Правильные метки — 5, 4, 9, 7.
Результат классификации — 6, 6, 4, 4.

Вывод: 

 Accuracy: 0.9164


На рисунке справа показаны четыре типичных изображения, на которых классификаторы ошибаются. Согласитесь, случаи действительно тяжелые.

Пример на языке Java

Пример классификации с применением weka.classifiers.functions.MultilayerPerceptron[7]

Maven зависимость: 

 <dependency>
   <groupId>nz.ac.waikato.cms.weka</groupId>
   <artifactId>weka-stable</artifactId>
   <version>3.8.0</version>
 </dependency>

 import weka.classifiers.functions.MultilayerPerceptron;
 import weka.core.converters.CSVLoader;
 import java.io.File;

 // read train & test datasets and build MLP classifier
 var trainds = new DataSource("etc/train.csv");
 var train   = trainds.getDataSet();
 train.setClassIndex(train.numAttributes() - 1);
 var testds = new DataSource("etc/test.csv");
 var test   = testds.getDataSet();
 test.setClassIndex(test.numAttributes() - 1);
 var mlp = new MultilayerPerceptron();
 mlp.buildClassifier(train);
 // Test the model
 var eTest = new Evaluation(train);
 eTest.evaluateModel(mlp, test);
 // Print the result à la Weka explorer:
 var strSummary = eTest.toSummaryString();
 System.out.println(strSummary);

См. также

Примечания

Источники информации

  • Сергей Николенко, Артур Кадурин, Екатерина Архангельская. Глубокое обучение. Погружение в мир нейронных сетей. — «Питер», 2018. — С. 93-123.
  • Нейронные сети — учебник
Источник — «http://neerc.ifmo.ru/wiki/index.php?title=Нейронные_сети,_перцептрон&oldid=85439»