Матрица инцидентности графа

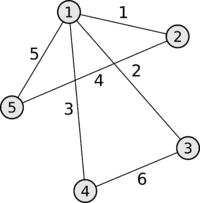
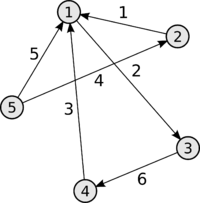
Определения для ориентированного и неориентированного графов

Определение:

Матрицей инцидентности (инциденций) (англ. Incidence matrix) неориентированного графа называется матрица [math]I (|V| \times |E|)[/math], для которой [math]I_{i,j} = 1[/math], если вершина [math]v_i[/math] инцидентна ребру [math]e_j[/math], в противном случае [math]I_{i,j} = 0[/math].

Определение:

Матрицей инцидентности (инциденций) (англ. Incidence matrix) ориентированного графа называется матрица [math]I (|V| \times |E|)[/math], для которой [math]I_{i,j} = 1[/math], если вершина [math]v_i[/math] является началом дуги [math]e_j[/math], [math]I_{i,j} = -1[/math], если [math]v_i[/math] является концом дуги [math]e_j[/math], в остальных случаях [math]I_{i,j} = 0[/math].

Свойства

Утверждение:

Для неориентированных графов без петель и кратных рёбер матрица инцидентности бинарна (состоит из нулей и единиц).

Утверждение:

Для ориентированных графов без петель и кратных рёбер матрица инцидентности состоит из нулей, единиц и [math]-1[/math].

Утверждение (о сумме элементов строки матрицы инцидентности для неориентированного графа):

Сумма элементов [math]i[/math]-й строки равна [math]deg \; v_i[/math].

Утверждение (о сумме элементов строки матрицы инцидентности для ориентированного графа):

Сумма элементов [math]i[/math]-й строки равна [math]deg^+ v_i - deg^- v_i[/math].

Пример

Граф	Матрица инцидентности	Ориентированный граф	Матрица инцидентности
	[math]\begin{pmatrix} 1 & 1 & 1 & 0 & 1 & 0\\ 1 & 0 & 0 & 1 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 1\\ 0 & 0 & 1 & 0 & 0 & 1\\ 0 & 0 & 0 & 1 & 1 & 0\\ \end{pmatrix}[/math]		[math]\begin{pmatrix} -1 & 1 & -1 & 0 & -1 & 0\\ 1 & 0 & 0 & -1 & 0 & 0\\ 0 & -1 & 0 & 0 & 0 & 1\\ 0 & 0 & 1 & 0 & 0 & -1\\ 0 & 0 & 0 & 1 & 1 & 0\\ \end{pmatrix}[/math]

См. также

• Матрица смежности графа

Источники

• Харари Фрэнк :Теория графов. Под ред. Л. Б. Штейнпресс. Изд. 2-е. — М.: Мир, 1973. — 180 с. — ISBN 5-354-00301-6
• Асанов М. О., Баранский В. А., Расин В. В.: Дискретная математика: графы, матроиды, алгоритмы — НИЦ РХД, 2001. — 288 с. — ISBN 5-93972-076-5
• Википедия — Incidence matrix