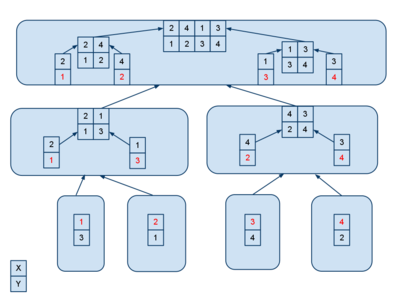
Сжатое многомерное дерево отрезков

Задача:

Пусть имеется множество [math]A[/math], состоящее из [math]n[/math] взвешенных точек в [math]p[/math]-мерном пространстве. Необходимо быстро отвечать на запрос о суммарном весе точек, находящихся в [math]p[/math]-мерном прямоугольнике [math](x_a,x_b),(y_a,y_b),\,...\,,(z_a,z_b)[/math]

Вообще говоря, с поставленной задачей справится и обычное [math]p[/math]-мерное дерево отрезков. Для этого достаточно на [math]i[/math]-той глубине вложенности строить дерево отрезков по всевозможным [math]i[/math]-тым координатам точек множества [math]A[/math], а при запросе для определения искомого отрезка использовать бинарный поиск.

Структура

Сжатое двумерное дерево отрезков, построенное по четырем точкам (x,y) на плоскости. Красным отмечены координаты, по которым производилась сортировка.

Вообще говоря, с поставленной задачей справится и обычное [math]p[/math]-мерное дерево отрезков. Если дерево строить по всем элементам массива, то запрос операции на [math]p[/math]-мерном прямоугольнике c помощью такой структуры будет выполняться за [math]O(\frac{1}{p}log^p\,S)[/math], а сама структура будет занимать порядка [math]O(S)[/math] памяти, где [math]S[/math] — количество элементов в [math]p[/math]-мерном массиве. Если дерево строить по элементам множества [math]A[/math], то асимптотики изменятся на [math]O(log^p\,n)[/math] и [math]O(n^p)[/math] соответственно. Однако, можно провести следующую оптимизацию — каждый раз дерево отрезков внутри вершины будем строить только по тем элементам множества [math]A[/math], которые встречаются в отрезке, за который отвечает эта вершина. Действительно, другие элементы уже были "исключены" и заведомо лежат вне желаемого [math]p[/math]-мерного прямоугольника. Для этого будем использовать сохранение всего подмассива в каждой вершине дерева отрезков.

Построение дерева и запрос операции

Алгоритм построения такого "усеченного" дерева отрезков будет выглядеть следующим образом:

• Cоставить массив из всех [math]n[/math] элементов множества [math]A[/math], упорядочить его по первой координате
• Построить на нём дерево отрезков с сохранением подмассива в каждой вершине
• Все подмассивы в вершинах получившегося дерева отрезков упорядочить по следующей координате, после чего повторить построение дерева для каждого из них

Псевдокод:

  build_normal_tree(element[] array)
  {
     //построение одномерного дерева отрезков на массиве array с сохранением подмассива в каждой вершине
  }
  
  get_inside_array(vertex)
  {
     //получение подмассива, сохраненного в вершине vertex
  }
  
  build_compressed_tree(element[] array, int coordinate = 0) 
  {
     //собственно, построение сжатого дерева отрезков
     if (coordinate < p) 
     {
        sort(array, coordinate); //сортировка массива по нужной координате
        segment_tree = build_normal_tree(array);
        for (each vertex in segment_tree) 
        {
           build_compressed_tree(inside_array(each), coordinate + 1);
        }
     }
  }

При такой оптимизации асимптотика размера структуры составит [math]O(n\,log^{p-1}\,n)[/math], а запрос будет аналогичен запросу в обычном [math]p[/math]-мерном дереве отрезков за [math]O(log^p\,n)[/math]. Но расплатой станет невозможность делать произвольный запрос модификации: в самом деле, если появится новый элемент, то это приведёт к тому, что мы должны будем в каком-либо дереве отрезков по второй или более координате добавить новый элемент в середину, что эффективно сделать невозможно.

Источники

Дерево отрезков на e-maxx.ru