Лемма о рукопожатиях
Неориентированный граф
| Лемма: |
Сумма степеней всех вершин графа (или мультиграфа без петель) — чётное число, равное удвоенному числу рёбер:
|
| Доказательство: |
| Возьмем пустой граф. Сумма степеней вершин такого графа равна нулю. При добавлении ребра, связывающего любые две вершины, сумма всех степеней увеличивается на 2 единицы. Таким образом, сумма всех степеней вершин чётна и равна удвоенному числу рёбер. |
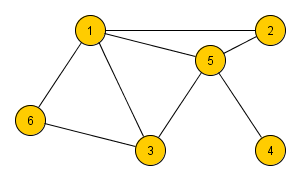
Например, для следующего графа выполнено:
Следствие 1. В любом графе число вершин нечётной степени чётно.
Следствие 2. Число рёбер в полном графе .
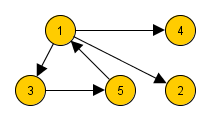
Ориентированный граф
| Лемма: |
Сумма входящих и исходящих степеней всех вершин ориентированного графа — чётное число, равное удвоенному числу рёбер:
|
| Доказательство: |
|
Аналогично доказательству леммы о рукопожатиях неориентированном графе. То есть возьмем пустой граф и будем добавлять в него рёбра. При этом каждое добавление ребра увеличивает на единицу сумму входящих и на единицу сумму исходящих степеней. Таким образом, сумма входящих и исходящих степеней всех вершин ориентированного графа чётна и равна удвоенному числу рёбер. |
Бесконечный граф
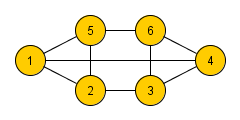
В бесконечном графе лемма не работает, даже в случае с конечным числом вершин нечётной степени. Покажем это на примере.
При выборе бесконечного пути из вершины (см. рисунок справа) имеем путь, в котором все вершины кроме стартовой имеют чётную степень, что противоречит следствию из леммы.
Регулярный граф
| Определение: |
| Граф называется регулярным, если степени всех его вершин равны. |
| Утверждение: |
В регулярном графе с вершинами ровно рёбер. |
| Утверждение: |
Если степень каждой вершины нечётна и равна , то количество рёбер кратно . |
| Действительно, так как степень каждой вершины нечётна, то число вершин в графе чётно(так сумма степеней всех вершин чётна). Пусть , то равенство принимает вид , то есть количество рёбер кратно . |
Источники информации
- Lecture Notes on Graph Theory By Tero Harju, Department of Mathematics University of Turku, 2011 — с. 7-8
- Handshaking lemma — Wikipedia