Теория Рамсея
Теория Рамсея — раздел математики, изучающий условия, при которых в произвольно формируемых математических объектах обязан появиться некоторый порядок.
Числа Рамсея
| Определение: |
| Клика (англ. clique) в неориентированном графе — подмножество вершин , такое что для любых двух различных вершин в существует ребро, их соединяющее. Другими словами, клика графа — полный подграф графа . |
| Определение: |
| Число Рамсея (англ. Ramsey's number) — наименьшее из таких чисел , что при любой раскраске ребер полного графа на вершинах в два цвета найдется клика на вершинах с ребрами цвета или клика на вершинах с ребрами цвета . |
Существует и другое определение для чисел Рамсея.
| Определение: |
| Число Рамсея — это наименьшее из всех таких чисел , что для любого графа на вершинах либо в найдется , либо в найдется граф . |
Несложно доказать, что данные определения эквивалентны. Достаточно показать, что раскрашенному в два цвета графу , можно однозначно поставить в соответствие граф на вершинах. Довольно часто определение для чисел Рамсея дается через задачу "о друзьях и незнакомцах"[1]. Пусть на вечеринке каждые два человека могут быть либо друзьями, либо незнакомцами, в общем виде задачи требуется найти, какое минимальное количество людей нужно взять, чтобы хотя бы человек были попарно знакомы, или хотя бы человек были попарно незнакомы. Если мы переформулируем данную задачу в терминах графов, то как раз получим определение числа Рамсея , представленное ранее.
Пример
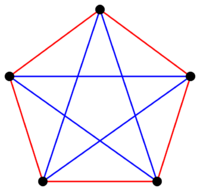
Чтобы получить лучшее представление природы чисел Рамсея, приведем пример. Докажем, что . Представим, что ребра раскрашены в два цвета: красный и синий. Возьмем вершину . Данной вершине, как и всем другим, инцидентны рёбер, тогда, согласно принципу Дирихле, хотя бы три из них одного цвета. Для определенности положим, что хотя бы ребра, соединяющие вершину с вершинами , , , синие. Если хотя бы одно из ребер , , синее, то в графе есть синий треугольник (полный граф на трёх вершинах), иначе, если они все красные, есть красный треугольник. Таким образом, . Чтобы доказать, что , предъявим такую раскраску графа , где нет клики на трех вершинах ни синего, ни красного цвета. Такая раскраска представлена на рисунке справа. Понятно, что предъявлять отдельные раскраски для , не нужно, так как достаточно взять соответствующие подграфы раскрашенного .
Теорема Рамсея. Оценки сверху
| Теорема (1, Теорема Рамсея): |
Для любых существует число , при этом , а также если числа и четные, то неравенство принимает вид . |
| Доказательство: |
|
| Утверждение (1): |
Для натуральных чисел выполняется равенство |
|
Очевидно, при или , как и соответствующие числа Рамсея. Индукцией по и при получаем |
Оценки снизу
| Теорема (2, Теорема Эрдеша): |
Для любого натурального числа выполняется неравенство |
| Доказательство: |
|
Так как , достаточно рассмотреть случай . Пусть доля среди помеченных графов на вершинах тех, что содержат клику на вершинах. Всего графов на наших вершинах, очевидно (каждое из возможных рёбер можно провести или не провести). Посчитаем графы с кликой на вершинах следующим образом: существует способов выбрать вершин для клики в нашем множестве, после чего все рёбра между ними будем считать проведенными, а остальные ребра выбираются произвольно. Таким образом, каждый граф с кликой на вершинах будет посчитан, причём некоторые даже более одного раза. Количестве графов с кликой оказывается не более, чем . Следовательно,
Подставив в неравенство мы получаем при Предположим, что и разобьём все графы на вершинах на пары . Так как , то существует пара , в которой ни , ни не содержат подграфа на вершинах. Рассмотрим раскраску рёбер в два цвета, в которой ребра цвета образуют граф . В такой раскраске нет клики на вершинах ни цвета , ни цвета , получили противоречие. Значит было выбрано неверно. Из этого следует . |
Свойства чисел Рамсея
Следующими свойствами удобно пользоваться при подсчете значений чисел Рамсея на практике.
Значения чисел Рамсея
Задача нахождения точных значений чисел Рамсея чрезвычайно трудна, их известно довольно мало. Далее приведена таблица Станислава Радзишевского, в которой присутствуют практически все известные числа Рамсея или же промежутки, в которых они находятся.
| Числа Рамсея | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
Числа Рамсея для раскрасок в несколько цветов
Теперь обобщим числа Рамсея на произвольное количество цветов.
| Определение: |
| Число Рамсея — это наименьшее из всех таких чисел , что при любой раскраске рёбер полного графа на вершинах в цветов для некоторого обязательно найдётся клика на вершинах с рёбрами цвета . |
| Теорема (3,Теорема Рамсея для нескольких цветов): |
существует число Рамсея , при этом |
| Доказательство: |
| Возьмем граф из вершин и окрасим его рёбра в цветов. Пока что будем считать цвета и одним цветом. Тогда граф будет -цветным. Согласно определению числа Рамсея , такой граф либо содержит для некоторого цвета , такого что , либо , окрашенный общим цветом и . В первом случае доказательство завершено. Во втором случае вернём прежние цвета и заметим, что, по определению числа Рамсея, полный — вершинный граф содержит либо цвета , либо цвета . Таким образом любое число Рамсея для раскраски в цветов ограничено некоторым числом Рамсея для меньшего количества цветов, следовательно, существует для любых , и теорема доказана. |
Числа Рамсея больших размерностей
| Определение: |
| Пусть , причём . Число Рамсея — наименьшее из всех таких чисел , что при любой раскраске -элементных подмножеств -элементного множества в цветов для некоторого обязательно найдётся такое множество , что и все -элементные подмножества множества имеют цвет . Число называют размерностью числа Рамсея . |
Заметим, что числа Рамсея размерности — это определённые ранее числа Рамсея для клик.
| Теорема (4, Теорема Рамсея для чисел больших размерностей): |
Пусть — натуральные числа, причем , а . Тогда существует число Рамсея . |
| Доказательство: |
|
Числа Рамсея для произвольных графов
Еще один способ обобщения классической теории Рамсея — замена клик на произвольные графы-шаблоны.
| Определение: |
| Пусть — графы. Число Рамсея — это наименьшее из всех таких чисел , что при любой раскраске рёбер полного графа на вершинах в два цвета обязательно найдется подграф, изоморфный с рёбрами цвета или подграф изоморфный с рёбрами цвета . |
Существует и другое определение чисел Рамсея для произвольных графов.
| Определение: |
| Пусть — графы. Число Рамсея — это наименьшее из всех таких чисел , что для любого графа на вершинах либо в найдется подграф изоморфный , либо в найдется подграф изоморфный . |
Несложно показать, что эти определения эквивалентны (аналогично определениям для классических чисел Рамсея). Из результатов классической теории Рамсея становится понятно, что числа существуют.
| Лемма (1): |
Пусть , а граф таков, что и , где — количество вершин в графе . Тогда граф содержит в качестве подграфа любое дерево на вершинах. |
| Доказательство: |
|
Зафиксируем и проведем индукцию по . База: для очевидно. Индукционный переход: Пусть верно для , докажем для . Рассмотрим произвольное дерево на вершинах, пусть дерево получено из удалением висячей вершины. Пусть — максимальное независимое множество вершин графа . Тогда , следовательно и очевидно . По индукционному предположению, граф содержит в качестве подграфа дерево . Пусть — вершина этого дерева, присоединив к которой висячую вершину, мы получим дерево . Заметим, что множество не является независимым ввиду максимальности . Следовательно, вершина смежна хотя бы с одной вершиной . Отметим, что не принадлежит множеству вершин графа и, присоединив вершину к вершине дерева , получим дерево в качестве подграфа графа . |
| Теорема (5, Теорема Хватала): |
, где — дерево на вершинах. |
| Доказательство: |
|
Сперва докажем, что . Для этого предъявим раскраску рёбер графа , в которой нет ни одного связного подграфа на вершинах с рёбрами цвета и нет клики на вершинах с рёбрами цвета . Разобьём вершины графа на клику по вершине и покрасим все рёбра этих клик в цвет . Тогда любой связный подграф с рёбрами цвета содержит не более вершины, в частности, нет подграфа с рёбрами цвета , изоморфного . Рёбра цвета (то есть, все оставшиеся рёбра) образуют -дольный граф, в котором, очевидно, нет клики на вершинах. Теперь воспользуемся вторым определением числа Рамсея . Рассмотрим произвольный граф на вершинах. Предположим, что в графе не существует клики на вершинах. Тогда и . По лемме , граф содержит в качестве подграфа любое дерево на вершинах, в частности, дерево, изоморфное . |
Индуцированная теорема Рамсея
| Определение: |
| Граф называется индуцированным подграфом (англ. induced subgraph) графа если две вершины в соединены ребром тогда и только тогда, когда они смежны в . |
| Определение: |
| Пусть — граф. Граф будем называть рамсеевским графом (англ. Ramsey’s graph) для , если при любой раскраске рёбер графа в два цвета существует одноцветный по рёбрам индуцированный подграф графа изоморфный . |
| Определение: |
| Индуцированным числом Рамсея (англ. induced Ramsey’s number) для графа будем называть минимальное число , такое что существует рамсеевский граф на вершинах для графа . |
Заметим, что при замене произвольного графа на клику мы получаем частный случай классической теоремы Рамсея.
| Теорема (6, Индуцированная теорема Рамсея): |
Для любого графа существует рамсеевский граф . |
Доказательство [2] данной теоремы было приведено независимо различными математиками, однако благодаря ему получилось предоставить только очень грубые оценки значений индуцированных чисел Рамсея. В данный момент проблема нахождения сколько-нибудь точных границ индуцированных чисел Рамсея является нерешенной задачей математики.
Особенности теории
Результаты, полученные в теории Рамсея, обладают двумя главными характеристиками. Во-первых, они не позволяют получить сами структуры: теоремы лишь доказывают, что они существуют, но алгоритма для их нахождения не предлагают. Единственным способ найти нужную конструкцию зачастую является перебор. Во-вторых, чтобы искомые структуры существовали, обычно требуется, чтобы объекты, их содержащие, состояли из очень большого числа элементов. Зависимость числа элементов объекта от размера конструкции обычно, как минимум, экспоненциальная.