Линейный клеточный автомат, эквивалентность МТ

Материал из Викиконспекты
Перейти к: навигация, поиск

Определения

Определение:
Клеточным автоматом (КА) (англ. cellular automaton) [math]A[/math] размерности [math]d[/math] называется четверка [math] \langle {Z^d}, S, N, \delta \rangle[/math], где
  • [math]S[/math] — конечное множество, элементы которого являются состояниями [math]A[/math].
  • [math]N[/math] — конечное упорядоченное подмножество [math]Z^d[/math], [math]N=\{{n_j} \mid {n_j}=(x_{1_j}, \dots, x_{d_j}), j \in \{1 \dots n\}\}[/math], называемое окрестностью (англ. neighborhood) [math]A[/math]. В данном определении полагается, что клетка всегда принадлежит своей окрестности.
  • [math]\delta : S^{n} \rightarrow S[/math] — функция перехода для [math]A[/math].


Определение:
Линейным клеточным автоматом (ЛКА) (англ. linear cellular automaton) называется одномерный клеточный автомат, окрестность каждой клетки которого состоит из [math]2 \cdot r + 1[/math] клеток, находящихся на расстоянии не более [math]r[/math] от данной.


Определение:
Состоянием покоя (англ. quiescent state) называется такое состояние автомата клетки [math]c[/math], что если автоматы клетки [math]c[/math] и всех ее соседей (клеток из ее окрестности) находятся в состояниях покоя, то автомат [math]c[/math] на следующем шаге останется в текущем состоянии.


Определение:
Спокойной клеткой (англ. quiescent cell) назовем клетку, автомат в которой перешел в состояние покоя.


Определение:
Конфигурацией (англ. configuraton) [math]c_i[/math] КА называется распределение состояний автоматов по клеточному пространству, где [math]i[/math] — шаг, после которого была получена конфигурация. Начальная конфиграция — [math]c_0[/math].


Определение:
Поддержкой (англ. support) конфигурации [math]c[/math] называется множество неспокойных клеток в ней. Обозначается [math]sup(c)[/math].


Другое определение линейного клеточного автомата

Определение:
Линейным клеточным автоматом [math]A[/math] назовем бесконечную ленту, в каждой клетке которой записан некоторый автомат. На вход автомату в клетке [math]i[/math] подается вектор из состояний автоматов в клетках с [math]i - r[/math] по [math]i + r[/math] включительно.
Лемма:
Для любого ЛКА можно построить эквивалентный ему ЛКА, во всех клетках которого будет записан один и тот же автомат.
Доказательство:
[math]\triangleright[/math]
Так как окрестность каждой клетки конечна и размер автомата в клетке конечен, то всего существует конечное число автоматов. Обозначим их множество как [math]D[/math]. Построим автомат [math]B[/math] следующим образом: множеством вершин [math]B[/math] будет объединение множеств вершин автоматов из [math]D[/math], переходы между вершинами [math]u[/math] и [math]v[/math] будут совпадать с переходами [math]D_i[/math], если [math]u[/math] и [math]v[/math] соответствуют вершинам из [math]D_i[/math], иначе переход отсутствует. Начальным состоянием автомата будет состояние,соответствующее начальному состоянию автомата [math]D_k[/math], который был записан в текущей клетке. Очевидно, что поведение такого автомата будет совпадать с поведением [math]D_k[/math].
[math]\triangleleft[/math]

Эквивалентность линейного клеточного автомата машине Тьюринга

Теорема:
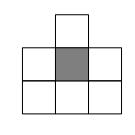
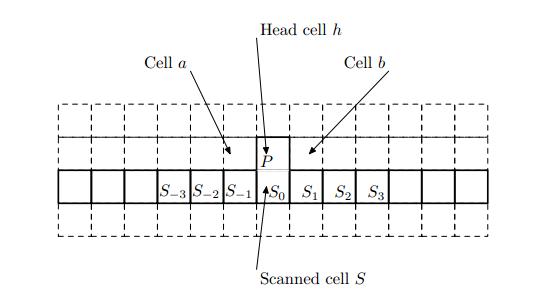
Для произвольной [math](m, n)[/math] машины Тьюринга [math]T[/math] существует двумерный КА с окрестностью из семи клеток и клеточным пространством [math]Z_T[/math] с [math]max(n + 1, m + 1)[/math] состояниями, симулирующий ее в реальном времени.
Доказательство:
[math]\triangleright[/math]
Рис. 1. Окрестность клетки

Каждому состоянию автомата клетки будет сопоставляться либо состояние автомата МТ, либо символ на ленте. Все клетки будут либо клетками ленты, расположенными в одном ряду, и в этом случае их состояние соответствует символу на ленте МТ, либо служебными клетками. Среди служебных клеток клетка [math]h[/math] будет соответствовать головке MT и в каждый момент находиться над какой-то клеткой ленты, клетки [math]a[/math] и [math]b[/math] всегда будут указывать на клетки слева и справа от [math]h[/math]. Остальные клетки будут находиться в состоянии покоя.

Заметим, что это порождает следующую проблему: размер входных данных МТ конечен, следовательно поддержка начальной конфигурации конечна. Так как МТ в общем случае может не остановиться, то в какой-то момент может потребоваться расширить ленту. Поэтому необходимо ввести две дополнительных служебных клетки, при необходимости расширяющих ленту влево или вправо (то есть переводящих соседнюю слева/справа клетку в свое состояние, а сами переходящие в состояние, соответствующее пустой клетке ленты МТ).

Построим окрестность, необходимую для корректной работы такого КА. Рассмотрев поведение МТ и зависимости клеток КА, получим, что минимальная по размеру окрестность имеет вид, представленный на Рис. 1.

Рис. 2. Эмуляция ленты МТ в КА
Также определим в каждой клетке состояние [math]w[/math], соответствующее начальному состоянию МТ. Перед началом эмуляции клетки ленты переведем в состояния эквивалентные входным символам, клетку над самой левой непустой клеткой ленты переведем в состояние [math]w[/math], которая будет соответствовать начальному положению головки. Тогда клетки ленты будут менять свои состояние так же, как лента МТ.
[math]\triangleleft[/math]
Теорема:
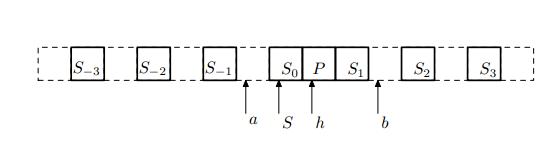
Для произвольной [math](m, n)[/math] машины Тьюринга существует линейный КА с окрестность не более, чем из шести клеток, [math]max(m + 1, n + 1)[/math] состояниями, эмулирующий эту МТ в реальном времени.
Доказательство:
[math]\triangleright[/math]

Лента будет иметь следующий вид:

Рис. 4. Эмуляция ленты МТ в ЛКА
Доказательство и построение автомата аналогично предыдущей теореме.
[math]\triangleleft[/math]
Теорема:
Для произвольного ЛКА можно построить эмулирующую его машину Тьюринга.
Доказательство:
[math]\triangleright[/math]
Пусть эмулируется ЛКА с окрестностью радиуса [math]d[/math] (из [math]2d + 1[/math] клетки). Пусть в автомате клетки всего [math]n[/math] состояний. Сопоставим каждому состоянию алфавита МТ, так что состояние покоя будет отображаться в пустую клетку ленты. Дополнительно введем символы-терминалы, указывающие на то, что соответствующие клетке ленты автоматы еще находятся в состояниях покоя. С точки зрения ЛКА клетки с терминалами будут считаться пустыми. Автомат МТ будет иметь [math]O(n^{2d+1})[/math] состояний — по состоянию для каждой возможной окрестности клетки, а также состояния, обеспечивающие правильную эмуляцию. Исходное состояние ленты МТ имеет следующий вид: отрезок, содержащий все клетки, эквивалентные неспокойным клеткам автомата, ограниченный с концов терминалами. Эмуляция каждой фазы ЛКА будет происходить следующим образом: головка будет сдвигаться до левого терминала, затем еще на [math]d[/math] влево. Затем левый терминал будет переноситься на [math]d[/math] клеток влево, а для каждой клетки правее нового положения левого терминала будет запоминаться ее окрестность, затем будет изменяться ее состояние соответственно поведению ЛКА. И так для всех клеток, пока не встретится правый терминал. В этом случае необходимо перенести его на [math]d[/math] клеток вправо и продолжить менять клетки до его следующего вхождения. Затем перейти к следующей фазе. Такая МТ будет эмулировать заданный ЛКА.
[math]\triangleleft[/math]

Из доказанных выше теорем следует, что линейный клеточный автомат и машина Тьюринга эквивалентны.

См. также

Источники информации

  • A.R. Smith III — Simple Computation-Universal Cellular Spaces, Journal of Association for Computing Machinery, Vol. 18, No. 3, July 1971.
  • M. Delorme — An Introduction to Cellular Automata, July 1998.
Источник — «http://neerc.ifmo.ru/wiki/index.php?title=Линейный_клеточный_автомат,_эквивалентность_МТ&oldid=85842»