Deepfake
Deepfake (дипфейк) — результат работы ряда алгоритмов для синтеза изображений человеческого лица или голоса. Основные алгоритмы применяемые для решения данной задачи основаны на Генеративно-состязательных сетях. Современные алгоритмы позволяют генерировать не только лицо человека, но и его голос. C таким примером можно ознакомится по ссылке [1]
Введение
Задача замены лиц или генерация Deepfake изображений состоит в том, чтобы перенести лицо с исходного (source) изображения на нужное (target) изображение. Такой перенос должен быть бесшовным и незаметным человеческому глазу. Реконструкция лица заключается в изменении лица из source изображения, так чтобы мимика и любая лицевая геометрия была соблюдена и соответствовала target изображению. Методы решаюшие данную задачу в прошлом были основаны на детектировании ключевых точек лица и соответствующей анимацией на основе построения триангуляции Делоне. В основе современных алгоритмов лежат Генеративно-Состязательные Сети с различными модификациями. Так же некоторые из используюмых методов используют основаны на попытке аппроксимации некого распределения признаков. Данные методы пытаются вычисляют данное распределение и переносят с помощью нейронных сетей эти скрытые представления в результате генерируется новое фотореалистичное лицо, которое соответствует необходимым характеристикам и метрикам.
Первые методы как было сказано выше были основаны на детектировании ключевых точек, одним из известных алгоритмов в этой области является Face2Face, метод вычисляет меш лица и с помощью алгоритма 3D morphable face model переносит геометрию. Методам на основе Генеративно-состязательных сетей не требуется никакие многоуровеные эвристические методы, они берут исходное изображение и сразу делают перенос в end-to-end стиле.
Реконструкция лица и сегментация
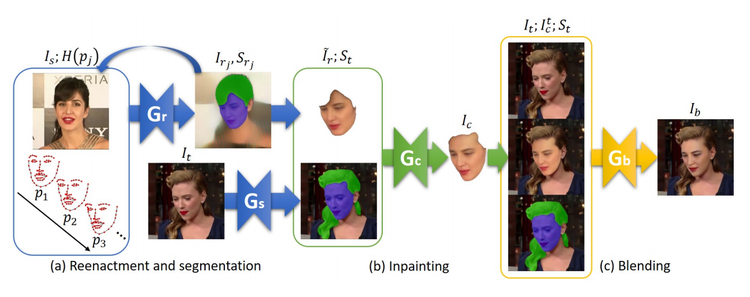
Первый этап рассмотренного алгоритма является сегментацией лица в target и source изображениях, изменение геометрии из source лица, чтобы оно соответствовало target геометрии лица. Имея изображение $I \in {\rm I\!R}^{3 \times H \times W}$ и тепловую карту лицевых точек $H(p) \in {\rm I\!R}^{N \times H \times W}, p \in {\rm I\!R}^{N \times D}$, где $N$ - число точек, $D$ - размерность точек, обычно она равна 2, а число точек не превышает 70, мы обучаем генератор, чтобы он делал трансформацию данной тепловой карты и входного изображения в изображение с необходимой нам геометрией $G_r : \{ {\rm I\!R}^{3 \times H \times W}, {\rm I\!R}^{N \times H \times W} \} \to {\rm I\!R}^{3 \times H \times W} $ Пусть $v_s, v_t \in {\rm I\!R}^{70 \times 3}$ и $e_s, e_t \in {\rm I\!R}^{3}$ будут $3$ мерными ключевыми лицевыми точками лица и углами Эйлера в соответствии к $F_s$ и $F_t$. Тогда мы построим 2D проекцию $p_j$ интерполируя между $e_s$ и $e_t$ и центроидами $v_s$ и $v_t$ и используя промежуточные точки мы обратно спроецируем $v_s$ на $I_s$. Другими словами алгоритм реконструкции является рекурсивным для каждой итерации
$i < j < n$
$I_{r_{j}}, S_{r_{j}} = G_r(I_{r_{j - 1}};H(p_j)), I_{r_{0}} = I_s$
Наша модель $G_r$ имеет 2 выхода, первый на выходе выдает изображение с перенесенной геометрией, второй выход маску для сегментации. Так же стоить заметить что маска для сегментации умеет различать часть лица с кожей и часть с волосами отдельно. Такой подход позволяет увеличить точность.
Такой генератор обучается следующую функцию потерь
$Loss(G_r) = \lambda_{stepwise} Loss_{rec}(I_{r_{n}}, I_{t}) + \lambda_{rec}Loss_{rec}(I_{r}, I_{t}) + \lambda_{adv}Loss_{adv} + \lambda_{seg}Loss_{pixel}(S_r, S_t)$
$Loss(G_s) = Loss_(CE) + \lambda_{reenact}Loss_{pixe}(S_t, S_{t}^{r})$
Где $G_r$ - генератор переноса геометрии, $G_s$ - генератор сегментации лица.
Перенос сгенерированного лица
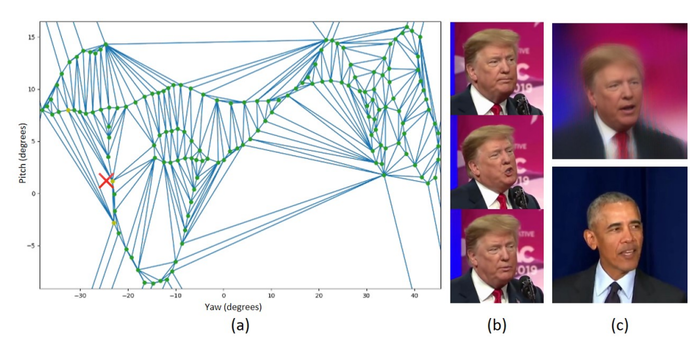
Общеизвестным способ переноса одной геометрии одной текстуры на другую является перенос полигонов из сеток с одной геометрии на другую. Однако существуют более современные способы. Имея множество исходных изображения $\{ I_{s_0}, ..., I_{s_{n}} \}$, углов Эйлера $ \{e_1, ..., e_n \}$ соответствующих лиц $\{ F_{s_{0}}, ..., F_{s_{n}} \}$ строится карта внешнего вида (appearance map). Строится она следующим образом. В начале проецируются соответствующие углы Эйлера на плоскость. Далее используя K-D дерево данные точки в пространстве сегментируются и удаляются слишком близкие, поскольку они не несут в себе много полезной информации, а вычислительная сложность разительно увеличивается. В конце используя оставшиеся точки мы строим меш лица используя триангуляцию Делоне. Для каждого угла $e_t$ лица $F_t$ и точки $x_t$ мы ищем треугольник $T$ соответствующий данной точке. Пусть $x_{i_{1}}, x_{i_{2}}, x_{i_{3}}$ будут трисом $T$ и $I_{s_{i_{1}}}, I_{s_{i_{2}}}, I_{s_{i_{3}}}$ соответствующие лица. Необходимо вычислить барицентрические координаты $\lambda_{1}, \lambda_{2}, \lambda_{3}$ от $x_t$ относительно $x_{i_{1}}, x_{i_{2}}, x_{i_{3}}$. Тогда результат интерполяции
$I_r = \sum_{k=1}^{3} \lambda_k G_r(I_{s_{i_{k}}}; H(p_t))$
где $p_t$ 2D ключевая точка лица $F_t$.
Вписывание лица
Поскольку из-за разницы в углах поворота или прически сегментированные маски могут отличаться видимыми регионами, поэтому нам необходимо "дорисовать" или "стереть" участки которые не могут быть перенесены напрямую. Чтобы решить данную задачу мы обучим еще одну модель $G_c$. $G_c$ принимает в себя лицо $F_s$, такое что все необходимые участки будут дорисованы, а ненужные удалены. Функция потерь такой сети
$Loss(G_c) = \lambda_{rec}Loss_{rec}(I_c, I_t) + \lambda_{adv}Loss_{adv}$
Отрисовка полученного лица
На самом последнем шаге мы уже имеем лицо которое правильно повернуто и на нем присутствуют только регионы лица, что и на нужном нам изображении. Нам остается только применить цветокоррекцию и последние минимальные правки чтобы отрисованное лицо выглядело натурально.
Пусть $I_t$ будет исходным лицом, а $I_{r}^{t}$ будет нужным нам лицом для переноса и $S_t$ маской сегментации. Тогда используя уравнене Пуассона мы можем выполнить цветокоррекцию следующим образом
$P(I_t;I_{r}^{t};S_t) = arg min ||\nabla f - \nabla I^{t}_{r}||^{2}_{2}$
$f(i, j) = I_t(i, j), \forall S_t(i, j) = 0$
$\nabla$ - оператор взятия градиента.
Данное уравнения используется в качестве функции для оптимизации нашего генератора $G_b$, который и будет заниматься отрисовкой финальной версии нашего Deepfake изображения.
$Loss(G_b) = \lambda_{rec}Loss_{rec}(I_t;I_{r}^{t};S_t), P(I_t;I_{r}^{t};S_t)) + \lambda_{adv}Loss_{adv}$
Данные для обучения и процесс обучения
В качестве обучающего множества можно использовать множество датасетов с размеченными лицами, одним из таких служит IJB-C. На нем обучается генератор $G_r$. Данный датасет состоит из более чем $11$ тысяч видео, $5500$ из которых выского качества. Обучая наш алгоритм кадры из $I_s$ и $I_t$ берутся из двух случайных видео. Так же для начального шага нам был необходим perceptual loss, он может быть получен обучив VGG-19 модель или взяв готовую обученную на ImageNet или VGGFace2, второй датасет предпочтительный, поскольку для его обучения используются только лица. В качестве оптимизатора рекомендуется использовать Adam с параметром скорости обучения (learning rate) = $0.0002$. $\lambda_{perc} = 1, \lambda_{pixel} = 0.1, \lambda_{adv} = 0.001, \lambda_{seg} = 0.1, \lambda_{stepwise} = 1$, параметр $\lambda_{reenact}$ возрастает линейно от $0-1$.
Общее время составляет около 2-3 дней на Nvidia Tesla V100. Скорость работы всего алгоритма состовляет около ~$10$ fps на Nvidia Tesla V100.
Реализация
Готовую реализацию можно найти по ссылке FSGAN, так же существуют альтернативные, но не менее продвинутые алгоритмы DeepFaceLab, faceswap.
Источники информации
- Nirkin, Yuval, Yosi Keller, and Tal Hassner. "FSGAN: Subject agnostic face swapping and reenactment." In Proceedings of the IEEE international conference on computer vision, pp. 7184-7193. 2019.
- Nirkin, Y., Masi, I., Tuan, A. T., Hassner, T., & Medioni, G. (2018, May). On face segmentation, face swapping, and face perception. In 2018 13th IEEE International Conference on Automatic Face & Gesture Recognition (FG 2018) (pp. 98-105). IEEE.