Циркуляция потока
Определение
<wikitex>
| Определение: |
| Циркуляцией называется поток в сети $G(V, E)$ нулевой величины. |
То есть закон сохранения потока должен выполняться для всех без исключения вершин графа. Фактически, нет нужды в истоке и стоке. </wikitex>
Постановка задачи
<wikitex>Рассмотрим сеть $G(V, E)$, в которой про каждое ребро $e_i$ известны величины: $l_i$ — минимальная пропускная способность и $c_i$ — максимальная пропускная способность. Необходимо выяснить, существует ли в этой сети циркуляция, удовлетворяющая требованиям, наложенным на пропускные способности.
Рассмотрим тривиальный случай, когда все $l_i = 0$, то достаточно пустить поток величины ноль из каждой вершины, что и будет ответом. Поэтому далее в графе будут существовать ребра с положительно нижней пропускной способностью. </wikitex>
Решение
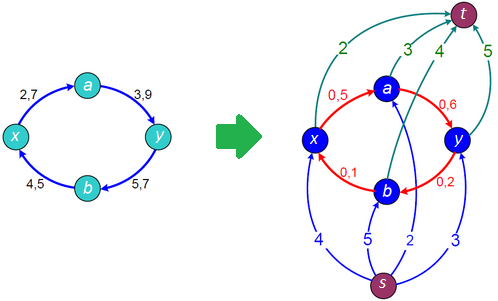
<wikitex>Для решения этой задачи нам понадобится изменить исходную сеть $G$ в $G'$ следующим образом. Сначала добавим в граф вершины $x$ — новый исток и $y$ — новый сток. Для каждого ребра $e_i = v_{from} \xrightarrow{l_i, c_i} v_{to}$ добавим ребра $x \xrightarrow{0, l_i} v_{to}$ и $u_{from} \xrightarrow{0, l_i} y$, а также сделаем в ребре $e_i$ изменения: $c_i = c_i - l_i, l_i = 0$.
Проанализируем новую сеть. Каждое ребро изначального графа мы заменили на три новых. Тот факт, что по изначальному ребру $e_i$ должен течь поток $l_i \leqslant f_i \leqslant c_i$ означает, что в новой сети по ребру $(x, v_{to})$ должен течь поток, равный $l_i$, то есть его пропускной способности. Поток, который раньше мог вытекать из $v_{from}$ по изначальному ребру, заменяется на поток, который может течь по ребрам $(v_{from}, v_{to})$ и $(v_{from}, y)$ (это ясно из того, что сумма их пропускных способностей в полученном графе равна $c_i$). То же самое верно и в вершине $v_{to}$, куда суммарный возможный входящий поток не изменился. Таким образом, ясно, что любой допустимый поток по любому ребру в изначальном графе можно распределить между тремя ребрами в полученном графе. Заметим, что в этом самом графе все $l_i = 0$, то есть мы имеем обыкновенную сеть.
От нас требовалось найти циркуляцию в исходной сети, то есть проверить, есть ли такой поток, что выполнено для всех вершин этого графа. Но это равносильно существованию потока между вершинами $x$ и $y$ в сети $G'$, который полностью насытит ребра, исходящие из истока. Действительно, этот факт будет означать, что этот поток в исходном графе насытит $i$-ое ребро как минимум на $l_i$, то и является нужным требованием. Если этот поток существует, то мы будем иметь:
- $\sum\limits_v f(u,v)=0,$ где $u \in V'-\{x,y\}, v \in V'$, то есть для всех исходных вершин;
- В $G': f_i \leqslant c_i - l_i \Rightarrow 0 \leqslant f_i \leqslant c_i - l_i \Rightarrow l_i \leqslant f_i \leqslant c_i$, то есть все удовлетворяет ограничениям.
то есть циркуляцию.
Запустим в новой сети один из алгоритмов поиска максимального потока. Если он не смог полностью насытить все ребра их истока, то и никакой другой по величине поток этого сделать не сможет, значит, циркуляции нет. Для получения величин потоков по каждому ребру изначальной сети в случае, если циркуляция есть, достаточно просто прибавить к потокам в ребрах $e'_i$ величины $l_i$. </wikitex>
Псевдокод
G // пустой граф, вершины 0 и n + 1 - исток и сток
n, m; // вершин, ребер в исходном графе
edge // ребро с полями (from, to, min_cap, cap)
Для i = 1 to m
считать ребро edge
добавить в граф G ребро (0, edge.to, 0, edge.min_cap)
добавить в граф G ребро (edge.from, edge.to, 0, edge.cap - edge.min_cap)
добавить в граф G ребро (edge.from, n + 1, 0, edge.min_cap)
max_flow = наибольший поток в графе G
Для всех ребер, инцидентных истоку
если для текущего ребра flow < cap
циркуляции НЕТ