Построение эквивалентного ДКА по НКА
Пусть нам дан произвольный НКА: [math]\langle \Sigma , Q, s \in Q, T \subset Q, \delta : Q \times \Sigma \to 2^Q \rangle[/math].
Построим по нему следующий ДКА: [math]\langle \Sigma , Q_d, s_d \in Q_d, T_d \subset Q_d, \delta_d : Q_d \times \Sigma \to Q_d \rangle[/math], где:
- [math]Q_d = 2^Q[/math],
- [math]s_d = \{s\}[/math],
- [math]T_d = \{q \in Q_d | \exists p \in T : p \in q\}[/math],
- [math]\delta_d(q, c) = \bigcup\limits_{a \in q} \delta(a, c)[/math].
Доказательство эквивалентности
| Теорема: |
Построенный ДКА эквивалентен данному НКА. |
| Доказательство: |
| [math]\triangleright[/math] |
- Докажем, что любое слово, которое принимает НКА, будет принято построенным ДКА. Заметим, что [math]\forall q \in q_d, \forall c \in \Sigma, \forall p \in \delta(q, c): p \in \delta_d(q_d, c)[/math]. Рассмотрим слово [math]w=w_1...w_m[/math], которое принимает автомат НКА: [math]\langle s, w_1w_2...w_m \rangle \vdash \langle u_1, w_2...w_m \rangle \vdash \langle u_m, \varepsilon \rangle, u_m \in T[/math]. Проверим, что построенный ДКА тоже принимает это слово. Заметим, что [math]s \in s_d[/math], а, значит, исходя из нашего наблюдения, мы получаем, что [math]u_1 \in {u_d}_1[/math], где [math]{u_d}_1 = \delta_d(s, w_1)[/math]. Далее, несложно заметить, что [math]\forall i \leq m : u_i \in {u_d}_i[/math], где [math]\langle s_d, w_1w_2...w_m \rangle \vdash \langle {u_d}_1, w_2...w_m \rangle \vdash \langle {u_d}_i, w_{i + 1}...w_m\rangle[/math]. Таким образом, [math]u_m \in {u_d}_m[/math], а из определения терминальных состояний в построенном ДКА мы получаем, что [math]{u_d}_m \in T_d[/math], то есть наш ДКА тоже принимает cлово [math]w[/math].
- Докажем, что любое слово, которое принимает построенный ДКА, принимает и НКА. Сначала сделаем наблюдение, что если [math]q_d=\{q\}[/math], и мы из него достигли по строке [math]S[/math] какого-то состояния [math]p_d[/math], то [math]\forall p \in p_d[/math] существует путь из [math]q[/math] в [math]p[/math] в НКА по строке [math]S[/math]. Рассмотрим слово [math]w=w_1...w_m[/math], которое принимает автомат ДКА: [math]\langle s_d, w_1w_2...w_m \rangle \vdash \langle {u_d}_1, w_2...w_m \rangle \vdash \langle {u_d}_m, \varepsilon \rangle, {u_d}_m \in T_d[/math]. Проверим, что НКА тоже принимает это слово. Так как [math]s_d = \{s\}[/math], и мы из [math]s_d[/math] достигли [math]{u_d}_m \in T_d[/math], возьмём любое терминальное состояние [math]u_m \in {u_d}_m[/math]. По нашему наблюдению в НКА есть путь из [math]s[/math] в [math]u_m[/math] по строке [math]w[/math], а, значит, НКА принимает это слово.
Таким образом, множества слов, допускаемых ДКА и НКА, совпадают, то есть они эквивалентны. |
| [math]\triangleleft[/math] |
Алгоритм Томпсона
Данный алгоритм преобразовывает НКА в эквивалентный ДКА. Будем использовать вышеуказанный способ построения с одним дополнением — не будем учитывать состояния недостижимые из стартового.
Поэтому в алгоритме используется обход в ширину.
Алгоритм
[math]Q[/math] — очередь состояний, соответствующих множествам, состоящих из состояний НКА.
[math]s[/math] — стартовое состояние НКА.
[math]Q[/math].push({[math]s[/math]})
while not isEmpty([math]Q[/math])
[math]Q[/math].pop([math]q_d[/math])
for [math]c \in \Sigma[/math]
[math]p_d[/math] = [math]\varnothing[/math]
for [math]q \in q_d[/math]
[math]p_d[/math] = [math]p_d \cup \delta(q, c)[/math]
if ([math]p_d[/math] haven't been in [math]Q[/math])
[math]Q[/math].push([math]p_d[/math])
Асимптотика
Так как количество подмножеств множества состояний НКА не более, чем [math]2^n[/math], а каждое подмножество мы обрабатываем ровно один раз за время [math]O(n)[/math], получаем верхнюю оценку времени работы алгоритма — [math]O(n \cdot 2^n)[/math].
Пример
Пусть нам дан недетерменированный конечный автомат: 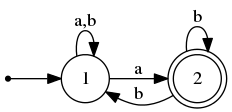
По нашему заданию эквивалентного ДКА мы получаем: 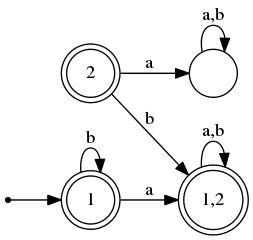
- Помещаем в очередь множество из одной стартовой вершины — [math]\{1\}[/math]: [math]Q = \{\{1\}\}[/math].
- Достаём из очереди множество [math]\{1\}[/math]: [math]Q = \{\}[/math].
- [math]q_d(\{1\}, a) = \{1, 2\}[/math], кладём множество [math]\{1, 2\}[/math] в очередь: [math]Q = \{\{1, 2\}\}[/math].
- [math]q_d(\{1\}, b) = \{1\}[/math], нам не надо класть множество [math]\{1\}[/math] в очередь, так как оно уже там было.
- Достаём из очереди множество [math]\{1, 2\}[/math]: [math]Q = \{\}[/math].
- [math]q_d(\{1, 2\}, a) = \{1, 2\}[/math], нам не надо класть множество [math]\{1, 2\}[/math] в очередь, так как оно уже там было.
- [math]q_d(\{1, 2\}, b) = \{1, 2\}[/math], нам не надо класть множество [math]\{1, 2\}[/math] в очередь, так как оно уже там было.
- Помечаем все терминальные вершины, в данном случае — [math]\{1, 2\}[/math].
В итоге получаем ДКА, эквивалентный исходному: 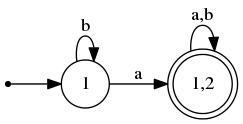 .
.


