Линейный клеточный автомат, эквивалентность МТ
Версия от 23:02, 23 января 2012; Alexey.tsyplenkov (обсуждение | вклад)
Определения
| Определение: |
Клеточным автоматом (КА) размерности называется четверка , где
|
| Определение: |
| Линейным клеточным автоматом (ЛКА) называется одномерный клеточный автомат, окрестность каждой клетки которого состоит из клеток, находящихся на расстоянии не более от данной. |
| Определение: |
| Состоянием покоя (quiescent state) называется такое состояние автомата , что если автомат перешел в состояние , то на следующем шаге он также будет находиться в состоянии . |
| Определение: |
| Спокойной клеткой (quiescent cell) назовем клетку, автомат в которой перешел в состояние покоя. |
| Определение: |
| Конфигурацией (configuraton) КА называется распределение состояний автоматов по клеточному пространству, где --- шаг, после которого была получена конфигурация. Начальная конфиграция---. |
| Определение: |
| Поддержкой (support) конфигурации называется множество неспокойных клеток в ней. Обозначается . |
| Определение: |
| Конфигурация называется пассивной (passive), если . |
| Определение: |
| Конфигурации называются непересекающимися (disjoint), если их поддержки не пересекаются как множества. |
Другое определение линейного клеточного автомата
| Определение: |
| Линейным клеточным автоматом назовем бесконечную ленту, в каждой клетке которой записан некоторый автомат. На вход автомату в клетке подается вектор из состояний автоматов в клетках с по включительно. |
| Утверждение: |
Для любого ЛКА можно построить эквивалентный ему ЛКА, во всех клетках которого будет записан один и тот же автомат. |
| Так как окрестность каждой клетки конечна и размер автомата в клетке конечен, то всего существует конечное число автоматов. Обозначим их множество как . Построим автомат следующим образом: множеством вершин будет объединение множеств вершин автоматов из , переходы между вершинами и будет совпадать с переходами , если и соответствуют вершинам из , иначе переход отсутствует. Начальным состоянием автомата будет состояние,соответствующее начальному состоянию автомата , который был записан в текущей клетке. Очевидно, что поведение такого автомата будет совпадать с поведением . |
Эквивалентность линейного клеточного автомата машине Тьюринга
| Лемма: |
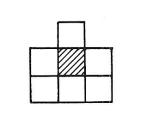
Для произвольной (m, n) машины Тьюринга существует двумерный КА с окрестностью из семи клеток и клеточным пространством с состояниями, симулирующий ее в реальном времени. |
| Доказательство: |
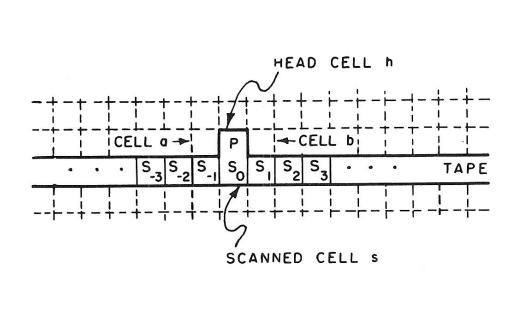
| Каждая клетка обладает множеством из состояний. Без потери общности, будем считать, что , так что будет сопоставляться символу машины Тьюринга при , а состояние будет соответствовать состоянию машины Тьюринга при . Ноль является состоянием покоя и не будет соответствовать символам и состояниям машины Тьюринга. Окрестность построим таким образом, чтобы выделять клетку, состояние которой будет соответствовать символу машины Тьюринга из клетки, состояние которой соответствует состоянию машины Тьюринга (окрестность клетки в таком КА показана на Рис. 1). Таким образом, симулирует машину Тьюринга, используя конфигурацию, в которой оно выглядит как машина Тьюринга. Один ряд клеток в представляет из себя ленту машины Тьюринга - одна клетка для каждой клетки ленты, а одна клетка из соседнего ряда будет соответствовать головке МТ. |