Теорема Понтрягина-Куратовского
Содержание
| Определение: |
| Граф гомеоморфен , если можно получить из с помощью конечного числа применений процедур включения и исключения вершин степени 2. |
| Теорема: |
Граф планарен тогда и только тогда, когда он не содержит подграфов, гомеоморфных или . |
| Доказательство: |
|
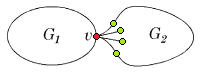
Доказательство необходимости можно посмотреть здесь, докажем достаточность. От противного: пусть существует непланарный граф, который не содержит подграфов, гомеоморфных или . Пусть — такой граф с наименьшим возможным числом рёбер, не содержащий изолированных вершин. G связенЕсли не связен, то его компоненты связности планарны и, следовательно, сам граф планарен. G — обыкновенный графВ самом деле, пусть в графе есть петля или кратное ребро . Тогда граф планарен. Добавляя ребро к графу получим, что граф он планарен. G — блокПусть, от противного, в графе есть точка сочленения . Через обозначим подграф графа , порождённый вершинами одной из компонент связности графа и вершинной , а через подграф графа , порождённый вершинами остальных компонент связности графа и вершиной . (рис. 1) Возьмём укладку графа на плоскости такую, что вершина лежит на границе внешней грани. Ее можно получить, взяв любую укладку на плоскости, по ней построив укладку на шаре, используя обратную [http://en.wikipedia.org/wiki/Stereographic_projection |
Литература
- Асанов М., Баранский В., Расин В. — Дискретная математика — Графы, матроиды, алгоритмы