Cортировка слиянием с использованием O(1) дополнительной памяти

Алгоритм слияния

На вход алгоритм получает массив, который состоит из двух отсортированных кусков:

Разобьем наш массив на блоки подряд идущих элементов длиной [math] \lfloor \sqrt{n} \rfloor [/math]. Остаток трогать не будем.

Найдем блок, содержащий конец первого отсортированного куска. Поменяем его с последним блоком. В дальнейшем будем использовать его как буфер обмена.

Отсортируем блоки по возрастанию по первому элементу (если первые элементы равны, тогда по последнему). Для этого подойдет любая квадратичная или более быстрая сортировка, которая требует дополнительной памяти [math] O (1) [/math]. Здесь нам выгодно использовать алгоритм, линейный по числу обменов, т.е. подходит сортировка выбором (selection sort).

Так как блоков [math] \sqrt{n} [/math], то количество операций на этом шаге [math] O(n) [/math].

Шаг 3

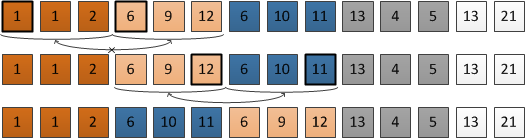
Попытаемся слить первую и вторую группу. Поменяем местами первую группу и часть остатка. И, как в обычном слиянии, пользуясь двумя указателями, сливаем вторую группу и только что измененную часть остатка. Результат начинаем записывать с начала первой группы. Чтобы ничего не перезаписалось, вместо записи используем обмен элементов. Так как группы имеют одинаковую длину, и между указателем на вторую группу и указателем на запись расстояние равно длине группы, то слияние произойдет корректно.

Пример : Пусть длины групп равны трем и [math] x_1\lt y_1\lt x_2\lt x_3\lt y_3 [/math], где первая группа [math] x_1,x_2,x_3 [/math] , а вторая [math] y_1,y_2,y_3. [/math]

Номер операции	Массив до выполнения операции	Массив после выполнения операции
1	[math][x_1,x_2,x_3,y_1,y_2,y_3,a_1,a_2,a_3] [/math]	[math][a_1,a_2,a_3,y_1,y_2,y_3,x_1,x_2,x_3] [/math]
2	[math][a_1,a_2,a_3,y_1,y_2,y_3,x_1,x_2,x_3] [/math]	[math][x_1,a_2,a_3,y_1,y_2,y_3,a_1,x_2,x_3] [/math]
3	[math][x_1,a_2,a_3,y_1,y_2,y_3,a_1,x_2,x_3] [/math]	[math][x_1,y_1,a_3,a_2,y_2,y_3,a_1,x_2,x_3] [/math]
4	[math][x_1,y_1,a_3,a_2,y_2,y_3,a_1,x_2,x_3] [/math]	[math][x_1,y_1,x_2,a_2,y_2,y_3,a_1,a_3,x_3] [/math]
5	[math][x_1,y_1,x_2,a_2,y_2,y_3,a_1,a_3,x_3] [/math]	[math][x_1,y_1,x_2,y_2,a_2,y_3,a_1,a_3,x_3] [/math]
6	[math][x_1,y_1,x_2,y_2,a_2,y_3,a_1,a_3,x_3] [/math]	[math][x_1,y_1,x_2,y_2,x_3,y_3,a_1,a_3,a_2] [/math]

Потом аналогично сольем вторую и третью группу и так до последней группы. Так как после второго шага количество инверсий для каждого элемента не больше [math] \sqrt{n} [/math], то ему надо сдвинуться влево не больше, чем на [math] \sqrt{n} [/math] элементов, поэтому в конце, не учитывая остаток, массив будет отсортированный.

Количество групп [math] \sqrt{n} [/math], и каждое слияние работает за [math] О O(\sqrt{n}) [/math] , поэтому количество операций на этом шаге [math] O(n) [/math] .

Шаг 4

Пусть размер остатка [math] s [/math]. Начиная с конца, разобьем наш массив на подряд идущие группы длиной s. Используя квадратичную или более быструю сортировку, которая требует дополнительной памяти [math] O(1) [/math], отсортируем подмассив длиной [math] 2s [/math], который находится в конце. На последних [math] s [/math] местах будут находиться s максимальных элементов. Оставшаяся часть представляет собой массив, содержащий две отсортированные части, причем размер второй равен [math] s [/math]. По аналогии с шагом 3 в обратном порядке сливаем группы длиной [math] s [/math].

Количество операций на этом шаге [math] O(n) [/math].

Шаг 5

Опять, используя экономную по памяти, хотя и квадратичную, сортировку, отсортируем:

1. остаток и первую группу.
2. последнюю группу.

Не стоит забывать, что после новой разметки остаток находится в начале, а не в конце.

В результате массив будет отсортированным

Количество операций на этом шаге [math] O(n) [/math].

Ссылки и литература

• Д.Е.Кнут - Искусство программирования (том 3) упр 18 к разделу 5.2.4
• Реализация алгоритма на JAVA