QpmtnriLmax
Постановка задачи
Рассмотрим еще одну задачу на нахождение расписания:
- У нас есть несколько машин, работающих параллельно. У всех машин разные скорости выполнения работ.
- Есть несколько заданий, каждое имеет своё время появления и время окончания .
- Работа может быть прервана и продолжена позже.
Требуется минимизировать опоздание
Алгоритм решения
Как в задаче сведем задачу к поиску потока сети. Также будем использовать бинарный поиск.
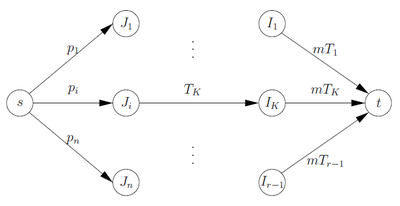
Пусть упорядоченная последовательность всех значений и . Определим произвольный интервал-узел на исходной сети (Рис. 1) для .
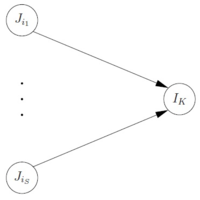
Расширим эту сеть. Обозначим через набор предшественников узла , тогда замененная нами подсеть (Рис. 2.1) определяется как . Расширение сети показано на Рис. 2.2.
Cчитаем, что станки индексируются в порядке невозрастания скоростей , кроме того .
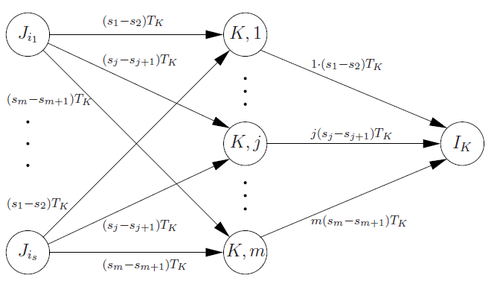
Расширенная подсеть строится путем добавления к вершинам вершин . При , есть дуги от до с емкостью и для всех и существует дуга из в с емкостью .
Для каждой вершины существуют вышеуказанные расширения. Кроме того, мы сохраняем дуги из в емкостью и дуги из в емкостью (Рис. 1).
| Теорема: |
Следующие свойства эквивалентны:
(a) Существует допустимое расписание. (b) В расширенной сети существует поток от до со значением |
| Доказательство: |
|
Рассмотрим в расширенной сети поток величиной . Обозначим через общий поток, который идет от до . Заметим, что . Достаточно показать, что для каждого подмножества выполняется . Это означает, что условие выполняется и требования к обработке могут быть запланированы как для . Рассмотрим подсеть в расширенной сети индуцированной и соответствующие части потока. Фрагмент частичного потока, который проходит через ограничен . Таким образом, мы имеем . (5.9) То, что равенство (5.9) справедливо, может рассматриваться как следствие. Если , то . В противном случае . Предположим, что допустимое расписание существует. Для и пусть является "объемом работ", который будет выполняться в интервале в соответствии с нашим возможным расписанием. Тогда для всех и произвольных наборов , неравенство (5.10) выполняется. Кроме того, для у нас . Остается показать, что можно отправить от до в расширенной сети. Такой поток существует, если и значение ограничено величиной минимального среза части сети с истоками и стоком . Тем не менее, это значение
Используя (5.10) и правую часть (5.9), получаем что и является искомым неравенством. |
Время работы
Работа с максимальным потоком в расширенной сети занимает шагов, проверка может быть сделана с такой же скоростью. Для решения мы используем бинарный поиск, получается алгоритм со сложностью , потому как , ограничен , при .
Задача представляет собой частный случай , и может быть решена более эффективно. Labetoulle, Lawler, Lenstra, и Rinnooy Kan разработали алгоритм работающий за специально для этого случая.
| Утверждение: |
Задача может быть решена за шагов. |
|
Решение эквивалентно нахождению наименьшего , такого, что задача с допустимым временным интервалом имеет решение. С другой стороны, решение эквивалентно нахождению такого наименьшего , такого, что задача с временным интервалом или имеет решение. |
Таким образом, задачи и симметричны.
Источники
- Peter Brucker. «Scheduling Algorithms» — «Springer», 2006 г. — 379 стр. — ISBN 978-3-540-69515-8