Эволюционные алгоритмы многокритериальной оптимизации, основанные на индикаторах. Гиперобъем

Эта статья находится в разработке!

Определение:

Задача многокритериальной оптимизации формулируется следующим образом: [math]\mathrm{maximize f(x)=(f_1(x), f_2(x),\ldots,f_d(x))}[/math], где [math]\mathrm{f(x):X \rightarrow R^d}[/math] ([math]d[/math] - количество критериев).

Надо заметить, что под термином [math]maximize[/math] мы понимаем оптимальность по Парето.

Определение:

Множество [math]X^* \subseteq X[/math] называется Парето оптимальным, если: [math]\mathrm{\forall x^* \subset X^* \not \exists x \subset X : x \succ x^*}[/math], где [math]\left(x \succ x^* \leftrightarrow \forall i \in 1 \ldots d: \left( f_i(x) \geq f_i(x^*)\right)\right) \bigwedge \left( \exists i \in 1 \ldots d: \left( f_i(x) \geq f_i(x^*)\right)\right) [/math]

Существует много различных индикаторов, с помощью которых численно оценивают качество множества решений. Но широко используется только один.

Определение:

Индикатор называется эластичным по Паретто(Pareto-compliant), если для любых двух множест решения [math]A[/math] и [math]B[/math] значение индикатора для [math]A[/math] больше значения для [math]B[/math] тогда и только тогда, когда [math]A[/math] доминирует [math]B[/math].

Дадим определение индикатора гиперобъема[math]\left(HYP\right)[/math].

Определение:

Пусть дано множество решения [math]\mathrm{X \in R^d}[/math]. Пусть также множество всех решений усечено некоторой точкой [math]\mathrm{r = \left(r_1, r_2, \ldots, r_d \right)}[/math]. Тогда: [math]\mathrm{HYP\left(X\right)=VOL\left( \bigcup\limits_{\left(x_1, x_2, \ldots, x_d \right) \in X} \left[ r_1, x_1\right] \times \left[ r_2, x_2\right] \times \cdots \times \left[ r_d, x_d\right] \right)}[/math], где через [math]VOL(X)[/math] обозначена мера множества [math]X[/math] по Лебегу.

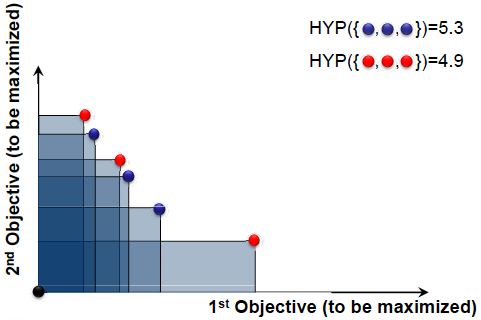
Пример:

Пусть [math]\mathrm{r = \left(0, 0, \ldots, 0 \right)}[/math] и [math]d=2[/math]. Тогда гиперобъем - это площадь объединения прямоугольников(см. рис).