Связь между максимизацией гиперобъема и аппроксимацией Парето-фронта
Содержание
Основные определения
| Определение: |
| Множество называется Парето оптимальным, если:
, где ( доминирует ) - множество оптимальных по Парето решений, его также называют Парето-фронтом. Парето-фронт не может быть вычислен за полиномиальное время. |
| Определение: |
| Множество решений называется -аппроксимацией функции , если:
Коэффицент аппроксимации функции на равен: аппроксимация Оптимальный коэффицент аппроксимации |
Свзяь между максимизацией гиперобъема и аппроксимацией Парето-фронта
Рассмотрим функции вида: , где убывает и . Коэффициент апроксимации монотонно убывающих функций не зависит от масштабов отрезков и . Так как для фиксированных констант функция и имеет тот же коэффициент аппроксимации. Однако, коэффициент аппроксимации зависит от значений и .
Множество всех таких функций обозначим через . Далее будем рассматривать только монотонно убывающие, полунепрерывные Парето-фронты. Условие полунепрерывности необходимо для того, чтобы существовало множество решение, максимизирующее индикатор гиперобъема.
Рассмотрим оптимальный коэффициент апроксимации для данного Парето-фронта из n () и верхнюю границу коэффициента аппроксимации для множества из n точек, максимизирующего значение индикатора гиперобъема () и докажем, что для количества точек они одинаковы, а именно .
Индикатор гиперобъема
| Определение: |
| Пусть дано множество решения . Пусть также множество всех решений усечено некоторой точкой . Тогда:
, где через обозначена мера множества по Лебегу. Гиперобъем является единственным унарным индикатором эластичным по Парето(Pareto-compliant). |
| Утверждение: |
Пусть .
Тогда существует, не обязятельно единственное, множество решения , которое максимизирует значение на |
| См. [Гиперобъем] |
Нахождение лучшего коэффициента аппроксимации
[Доказательство] ограничивает значение оптимального коэффицента апроксимации сверху: = .
Нахождение коэффициента аппроксимации множества решения максимизируюшего гиперобъем
| Утверждение: |
Пусть и .
Тогда [MINCON] данного множество решения: |
|
Исходя из определения минимальный вклад в гиперобъем множества равен минимуму из всевозможных площадей прямоугольников, образующихся между соседними точками множества решения и их значенияями. Пусть - длины сторон соответствующего прямоугольника, тогда:
Это означает:
и поэтому: Так как среднее гармоническое меньше чем среднее арифметическое: Преобразуя, получаем искомое. |
Далее необходимо посчитать коэффициент аппроксимации для внутренних и внешних точек
| Утверждение: |
Пусть и .
Тогда [MINCON] данного множество решения: |
|
Исходя из определения минимальный вклад в гиперобъем множества равен минимуму из всевозможных площадей прямоугольников, образующихся между соседними точками множества решения и их значенияями. Пусть - длины сторон соответствующего прямоугольника, тогда:
Это означает:
и поэтому: Так как среднее гармоническое меньше чем среднее арифметическое: Преобразуя, получаем искомое. |
В статье [1], п. 4 приведено доказательство того, что для данного вида функций всегда существует множество решение, максимизирующее значение индикатора гиперобъема, а также устанавливает значение коэффициент аппроксимации значением: = .
Примечание
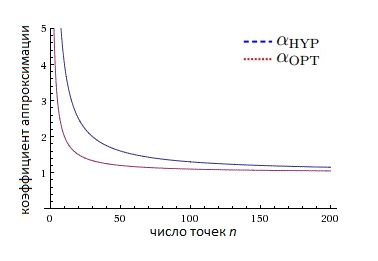
Конечно, зависимость от и в аппроксимационном коэффициенте оптимального множества решения меньше чем в аппроксимационном коэффициенте для множества, максимизирующего гиперобъем. Однако, полученная граница для коэффициента аппроксимации является верхней. На рисунке ниже Вы можете увидеть пример поведения данных значений для определенного класса функций.