Задача многокритериальной оптимизации. Multiobjectivization
Содержание
Задача многокритериальной оптимизации
Постановка задачи
| Определение: |
| Задача многокритериальной оптимизации:
|
Так как не существует единого решение, которое было бы максимальным для всех целевых функций, вместо него можно искать множество множество Парето оптимальных значений.
Множество Парето оптимальных значений
| Определение: |
Множество Парето оптимальных значений:
|
Выражение означает, что доминирует над .
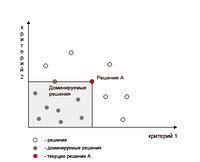
Говорят, что доминирует над . по Парето, если не хуже по всем критериям и хотя бы по одному критерию превосходит . В таком случае в выборе нет смысла, т.к. по всем параметрам не уступает, а по каким-то и превосхожит . Если рассматривать всего два критерия то на рис. 1 показана область пространства, доминируемая данным решением А. Эта область «замкнута»: элементы на ее границе также доминируемы А
| Определение: |
| Для двух решений и говорят тогда и только тогда, когда – такую пару решений называют недоминируемой |
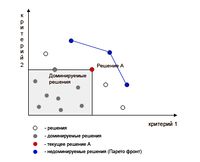
На рис. 2 показана граница Парето для возможных решений в двухкритериальном пространстве
Множество Парето оптимальных недоминируемых решений называется Парето фронтом.
Multi-objectivization
Суть метода мульти-объективизации заключается в разбитии сложной задачи с одной целевой функцией на несколько подзадач, найти для каждой подзадачи решение и выбрать оптимальное решение.
Для выполнения оптимизации многокритериальной задачи мы должны добавить в целевую функцию новые параметры, либо должны добавить новые целевые функции.
Сложность этой процедуры заключается в разложении проблемы на ряд мелких независимых между собой подпроблем.
Алгоритмы
Hill-Climbers
| Определение: |
| Hill-Climbers – Итеративный алгоритм, который начинается с произвольного решения проблемы, а затем пытается найти лучшее решение, постепенно изменяя его. Если изменения позволяют найти лучшее решение, алгоритм сохраняет его и повторяет и повторяет своё выполнение до тех пор, пока лучшие решения не могут быть найдены |
| Initialization: | Init_pop |
| Main Loop: | Rand_mem,Rand_mem Mutate,Mutate
if if |
| Termination: | return Best |
Задачи
Задача коммивояжера (TSP)является наиболее известно из всего класса -сложных задач. Формулируется задача следующим образом:
Задано – множество городов и для каждой пары задано расстояние. Наша цель – найти цепь из городов, минимизирующую величину:
Для того, чтобы объектизировать эту задачу, нам необходимо определить подзадачи. TSP – является -сложной именно потому, что нет хорошего разложения этой задачи.
Приведем алгоритм для задачи коммивояжера на основе "жадной" стратегии:
- Для каждой пары хромосом случайным образом выберем точку разрыва и в качестве номера стартовой вершины возьмем номер отмеченного гена в хромосоме.
- Сравним частичную стоимость путей, ведущих из текущих вершин в хромосомах родителях, и выберем из них кратчайший.
- Если выбранная таким образом вершина графа уже была включена в частичный путь, то взять случайную вершину из числа не просмотренных. Присвоить полученной вершине значение текущей.
- При преждевременном образовании циклов выбирается другой кратчайший путь.
- Повторяем пункты 2 и 3 пока не будет просмотрен гамильтонов цикл с квазиминимальной суммарной стоимостью рёбер.
- Конец работы алгоритма
Для того, чтобы избежать проблемы локального минимума, в алгоритм вводится модификация:
- Предпочтение более невыгодного маршрута с точки зрения заданной целевой функции более выгодному отдается с определенной вероятностью.
- выбирается около половины генетического материала от каждого из родителей