Разрешение коллизий

Определение:

Коллизия хеш-функции — это равенство значений хеш-функции на двух различных блоках данных.

Разрешение коллизий в хеш-таблице, задача, решаемая несколькими способами. Можно использовать списки, а можно открытую адресацию.

При использовании списков особых проблем не возникает, так как там в каждой ячейке хранится список всех элементов. При добавлении необходимо просто добавить элемент в начало списка.

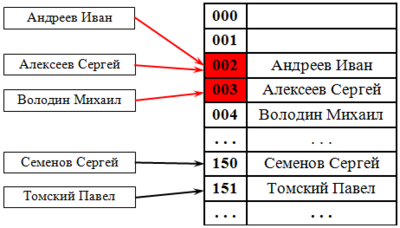
При открытой адресации будет иначе: в каждой ячейке хеш-таблицы хранится только один элемент. Тогда при добавлении, если ячейка свободна, мы просто записываем добавляемый элемент в эту ячейку. Однако если эта ячейка занята — необходимо поместить добавляемый элемент в какую-нибудь другую свободную ячейку. Такие ситуации нередки, так как невозможно использовать хеш-функцию, не дающую коллизий, а каждой ячейке таблицы соответствует одно значение хеш-функции. Далее мы рассмотрим несколько стратегий поиска свободного места в данном случае.

Стратегии поиска

Последовательный поиск

При попытке добавить элемент в занятую ячейку $i$ начинаем последовательно просматривать ячейки $i+1, i+2, i+3$ и так далее, пока не найдём свободную ячейку. В неё и запишем элемент.

Линейный поиск

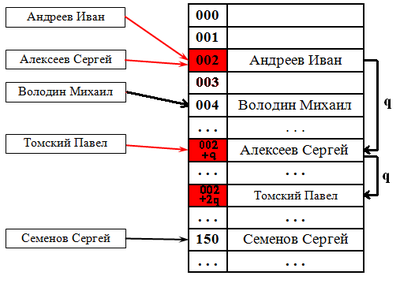
Выбираем шаг $q$. При попытке добавить элемент в занятую ячейку $i$ начинаем последовательно просматривать ячейки $i+(1 \cdot q), i+(2 \cdot q), i+(3 \cdot q)$ и так далее, пока не найдём свободную ячейку. В неё и запишем элемент. По сути последовательный поиск - частный случай линейного, где $q=1$.

Квадратичный поиск

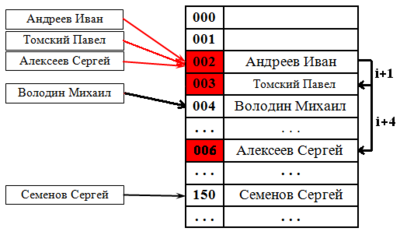
Шаг $q$ не фиксирован, а изменяется квадратично: $q = 1,4,9,16...$. Соответственно при попытке добавить элемент в занятую ячейку $i$ начинаем последовательно просматривать ячейки $i+1, i+4, i+9$ и так далее, пока не найдём свободную ячейку.

Проверка наличия элемента в таблице

Проверка осуществляется аналогично добавлению: мы проверяем ячейку $i$ и другие, в соответствии с выбранной стратегией, пока не найдём искомый элемент или свободную ячейку.

При поиске элемента может получится так, что мы дойдём до конца таблицы. Обычно поиск продолжается, начиная с другого конца, пока мы не придём в ту ячейку, откуда начинался поиск.

Проблемы данных стратегий

Проблем две — крайне нетривиальное удаление элемента из таблицы и образование кластеров — последовательностей занятых ячеек.

Кластеризация замедляет все операции с хеш-таблицей: при добавлении требуется перебирать всё больше элементов, при проверке тоже. Чем больше в таблице элементов, тем больше в ней кластеры и тем выше вероятность того, что добавляемый элемент попадёт в кластер. Для защиты от кластеризации используется Двойное хеширование и хеширование кукушки.

Удаление элемента без пометок

Рассуждение будет описывать случай с линейным поиском хеша. Будем при удалении элемента сдвигать всё последующие на $q$ позиций назад. При этом:

• если в цепочке встречается элемент с другим хешем, то он должен остаться на своём месте (такая ситуация может возникнуть если оставшаяся часть цепочки была добавлена позже этого элемента)
• в цепочке не должно оставаться "дырок", тогда любой элемент с данным хешем будет доступен из начала цепи

Учитывая это будем действовать следующим образом: при поиске следующего элемента цепочки будем пропускать все ячейки с другим значением хеша, первый найденный элемент копировать в текущую ячейку, и затем рекурсивно его удалять. Если такой следующей ячейки нет, то текущий элемент можно просто удалить, сторонние цепочки при этом не разрушатся (чего нельзя сказать про случай квадратичного поиска).

Псевдокод

  delete(i) 
     j = i + q
     while table[j] == null || table[j].key != table[i].key
        if (table[j] == null)
           table[i] = null
           exit
        j += q
     table[i] = table[j]
     delete(j);      

Хеш-таблицу считаем зацикленной

Утверждение (о времени работы):

Асимптотически время работы $delete$ и $find$ совпадают

$\triangleright$

Заметим что указатель $j$ в каждой итерации перемещается вперёд на $q$ (с учётом рекурсивных вызовов $delete$). То есть этот алгоритм последовательно пройдёт по цепочке от удаляемого элемента до последнего - с учётом вызова $find$ собственно для нахождения удаляемого элемента, мы посетим все ячейки цепи.

$\triangleleft$

Вариант с зацикливанием мы не рассматриваем, поскольку если $q$ взаимнопросто с размером хеш-таблицы, то для зацикливания в ней вообще не должно быть свободных позиций

Теперь докажем почему этот алгоритм работает. Собственно нам требуется сохранение трёх условий.

• В редактируемой цепи не остаётся дырок

Докажем по индукции. Если на данной итерации мы просто удаляем элемент (база), то после него ничего нет, всё верно. Если же нет, то вызванный в конце $delete$ (см. псевдокод) заметёт созданную дыру (скопированный элемент), и сам, по предположению, новых не создаст.

• Элементы, которые уже на своих местах, не должны быть сдвинуты.

Это учтено.

• В других цепочках не появятся дыры

Противное возможно только в том случае, если какой-то элемент был действительно удалён. Удаляем мы только последнюю ячейку в цепи, и если бы на её месте возникла дыра для сторонней цепочки, это бы означало что элемент, стоящий на $q$ позиций назад, одновременно принадлежал нашей и другой цепочкам, что невозможно.

Двойное хеширование

Двойное хеширование — метод борьбы с коллизиями, возникающими при открытой адресации, основанный на использовании двух хеш-функций для построения различных последовательностей исследования хеш-таблицы.

Принцип двойного хеширования

При двойном хешировании используются две независимые хеш-функции $h_1(k)$ и $h_2(k)$. Пусть $k$ — это наш ключ, $m$ — размер нашей таблицы, $n \mod m$ — остаток от деления $n$ на $m$, тогда сначала исследуется ячейка с адресом $h_1(k)$, если она уже занята, то рассматривается $(h_1(k) + h_2(k)) \mod m$, затем $(h_1(k) + 2 \cdot h_2(k)) \mod m$ и так далее. В общем случае идёт проверка последовательности ячеек $(h_1(k) + i \cdot h_2(k)) \mod m$ где $i = (0, 1, \; ... \;, m - 1)$

Таким образом, операции вставки, удаления и поиска в лучшем случае выполняются за $O(1)$, в худшем — за $O(m)$, что не отличается от обычного линейного разрешения коллизий. Однако в среднем, при грамотном выборе хеш-функций, двойное хеширование будет выдавать лучшие результаты, за счёт того, что вероятность совпадения значений сразу двух независимых хеш-функций ниже, чем одной.

$\forall x \neq y \; \exists h_1,h_2 : p(h_1(x)=h_1(y))\gt p((h_1(x)=h_1(y)) \land (h_2(x)=h_2(y)))$

Выбор хеш-функций

$h_1$ может быть обычной хеш-функцией. Однако чтобы последовательность исследования могла охватить всю таблицу, $h_2$ должна возвращать значения:

• не равные $0$
• независимые от $h_1$
• взаимно простые с величиной хеш-таблицы

Есть два удобных способа это сделать. Первый состоит в том, что в качестве размера таблицы используется простое число, а $h_2$ возвращает натуральные числа, меньшие $m$. Второй — размер таблицы является степенью двойки, а $h_2$ возвращает нечетные значения.

Например, если размер таблицы равен $m$, то в качестве $h_2$ можно использовать функцию вида $h_2(k) = k \mod (m-1) + 1$

Вставка при двойном хешировании

Пример

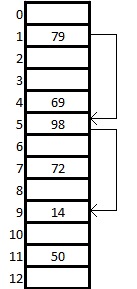
Показана хеш-таблица размером 13 ячеек, в которой используются вспомогательные функции:

$h(k,i) = (h_1(k) + i \cdot h_2(k)) \mod 13$

$h_1(k) = k \mod 13$

$h_2(k) = 1 + k \mod 11$

Мы хотим вставить ключ 14. Изначально $i = 0$. Тогда $h(14,0) = (h_1(14) + 0\cdot h_2(14)) \mod 13 = 1$. Но ячейка с индексом 1 занята, поэтому увеличиваем $i$ на 1 и пересчитываем значение хеш-функции. Делаем так, пока не дойдем до пустой ячейки. При $i = 2$ получаем $h(14,2) = (h_1(14) + 2\cdot h_2(14)) \mod 13 = 9$. Ячейка с номером 9 свободна, значит записываем туда наш ключ.

Таким образом, основная особенность двойного хеширования состоит в том, что при различных $k$ пара $(h_1(k),h_2(k))$ дает различные последовательности ячеек для исследования.

Простая реализация

Пусть у нас есть некоторый объект $item$, в котором определено поле $key$, от которого можно вычислить хеш-функции $h_1(key)$ и $h_2(key)$

Так же у нас есть таблица $table$ величиной $m$, состоящая из объектов типа $item$.

Вставка

add(item)
   x = h1(item.key)
   y = h2(item.key)
   for (i = 0; i < m; i++)    	
      if table[x] == null
         table[x] = item
         return      
      x = (x + y) mod m   
   table.resize() //ошибка, требуется увеличить размер таблицы

Поиск

search(key)
   x = h1(key)
   y = h2(key)
   for (i = 0; i < m; i++)
      if table[x] != null
         if table[x].key == key
            return table[x]
      else
         return null
      x = (x + y) mod m   
   return null

Реализация с удалением

Что бы наша хеш-таблица поддерживала удаление, требуется добавить массив $deleted$ типов $bool$, равный по величине массиву $table$. Теперь при удалении мы просто будем помечать наш объект как удалённый, а при добавлении как не удалённый и замещать новым добавляемым объектом. При поиске, помимо равенства ключей, мы смотрим, удалён ли элемент, если да, то идём дальше.

Вставка

add(item)
   x = h1(item.key)
   y = h2(item.key)
   for (i = 0; i < m; i++)   	
      if table[x] == null || deleted[x]
         table[x] = item
         deleted[x] = false
         return      
      x = (x + y) mod m   
   table.resize() //ошибка, требуется увеличить размер таблицы

Поиск

search(key)
   x = h1(key)
   y = h2(key)
   for (i = 0; i < m; i++) 
      if table[x] != null
         if table[x].key == key && !deleted[x]
            return table[x]
      else
         return null
      x = (x + y) mod m   
   return null

Удаление

remove(key)
   x = h1(key)
   y = h2(key)
   for (i = 0; i < m; i++)
      if table[x] != null
         if table[x].key == key
            deleted[x] = true
      else 
         return
      x = (x + y) mod m

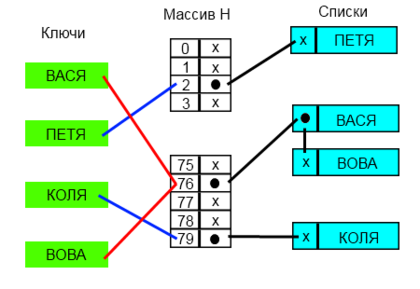
Разрешение коллизий с помощью списков

Каждая ячейка $i$ массива $H$ содержит указатель на начало списка всех элементов, хеш-код которых равен $i$, либо указывает на их отсутствие. Коллизии приводят к тому, что появляются списки размером больше одного элемента.

Время, необходимое для вставки в наихудшем случае равно $O(1)$. Это операция выполняет быстро, так как считается, что вставляемый элемент отсутствует в таблице, но если потребуется, то перед вставкой мы можем выполнить поиск этого элемента.

Время работы поиска в наихудшем случае пропорционально длине списка, а если все $n$ ключей захешировались в одну и ту же ячейку (создав список длиной $n$) время поиска будет равно $\Theta(n)$ плюс время вычисления хеш-функции, что ничуть не лучше, чем использование связного списка для хранения всех $n$ элементов.

Удаления элемента может быть выполнено за $O(1)$, как и вставка, при использовании двухсвязного списка.

См. также

• Хеширование
• Хеширование кукушки

Литература

• Бакнелл Дж. М. Фундаментальные алгоритмы и структуры данных в Delphi, 2003
• Кнут Д. Э. Искусство программирования, том 3. Сортировка и поиск, 2-е издание, 2000
• Томас Кормен, Чарльз Лейзерсон, Рональд Ривест, Клиффорд Штайн. Алгоритмы. Построение и анализ, 2010
• Седжвик Р. Фундаментальные алгоритмы на C. Части 1-4. Анализ. Структуры данных. Сортировка. Поиск, 2003

Ссылки

• Wikipedia — Double_hashing
• Разрешение коллизий
• Пример хеш таблицы
• Пример хеш таблицы с двойным хешированием