J2ni2Cmax

Постановка задачи

Рассмотрим задачу:

1. Дано $n$ работ и $2$ станка.
2. Для каждой работы известно её время выполнения на каждом станке $p_{ij}$.
3. Для каждой работы известна последовательность $O_{ik}$ станков - порядок, в котором нужно выполнить работу.
4. Для любой работы $n_{i}$ (Длина последовательности $O_{i}$) $\lt =2$.

Требуется минимизировать время окончания выполнения всех работ.

Описание алгоритма

$M_{1}$ - первый станок. $M_{2}$ - второй станок.

Разобьем все работы на четыре множества:

1. $I_{1}$ - множество всех работ, которые должны выполниться только на $M_{1}$.
2. $I_{2}$ - множество всех работ, которые должны выполниться только на $M_{2}$.
3. $I_{12}$ - множество всех работ, которые должны выполниться сначала на $M_{1}$ затем на $M_{2}$.
4. $I_{21}$ - множество всех работ, которые должны выполниться сначала на $M_{2}$ затем на $M_{1}$.

Решим задачу $F2 \mid \mid C_{max}$ для $I_{12}$ и для $I_{21}$ независимо. Получим расписание $S_{12}$ и $S_{21}$.

Тогда оптимальное расписание для нашей задачи будет следующим:

• Расписание $M_{1}$ : сначала $I_{12}$ в соответсвии с расписанием $S_{12}$. Затем $I_{1}$ в произвольном порядке. Затем $I_{21}$ в соответсвии с $S_{21}$.
• Расписание $M_{2}$ : сначала $I_{21}$ в соответсвии с расписанием $S_{21}$. Затем $I_{2}$ в произвольном порядке. Затем $I_{12}$ в соответсвии с $S_{12}$.

Примечание: во время выполнения $I_{21}$ на $M_{1}$ или $I_{12}$ на $M_{2}$ могут возникнуть простои из-за того, что работа ещё не выполнилась на предыдущем станке.

Доказательство корректности алгоритма

$T_{j}(x)$ - время выполнения множества работ $x$ на станке $j$.

$G_{j}$ - множество всех работ, которые нужно сделать хотя бы раз на $j$-м станке. (Формально $G_{1} = I_{1} \cup I_{12} \cup I_{21}$)

Лемма:

Расписание, построенное данным алгоритмом, обладает следующим свойством : один из станков работает без простоев.

Доказательство:

$\triangleright$

Рассмотрим 2 случая: $T_{1}(I_{12}) + T_{1}(I_{1}) \gt = T_{2}(I_{21})$. Тогда $M_{1}$ работает без прерываний, т.к к моменту завершения выполнения $I_{1}$ на $M_{1}$ все работы $I_{21}$ выполнены на $M_{2}$. Иначе $T_{1}(I_{12}) + T_{1}(I_{1}) \lt T_{2}(I_{21})$. Тогда $M_{2}$ работает без прерываний, т.к к моменту завершения выполнения $I_{2}$ на $M_{2}$ все работы $I_{12}$ выполнены на $M_{1}$ .

$\triangleleft$

Теорема:

Расписание, построенное данным алгоритмом, является корректным и оптимальным.

Доказательство:

$\triangleright$

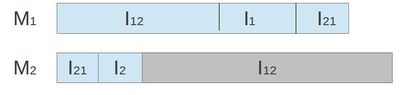Рис. 1 - Расположение работ. В серой области могут быть прерывания. Корректность алгоритма очевидна. Докажем оптимальность. Пусть, для опеределенности $M_{1}$ работает без прерываний. Рассмотрим станок на котором достигается $C_{max}$ . Если это $M_{1}$, то оптимальность очевидна ($C_{max} \gt = \sum\limits_{i \in G_{1}} p_{i1}$). Иначе $C_{max}$ достигается на $M_{2}$. Тогда либо $M_{2}$ работает без прерываний и оптимальность очевидна. Или есть прерывания. Тогда целевая функция равна ответу задачи $F2 \mid \mid C_{max}$ для работ $I_{21}$, который оптимален.

$\triangleleft$

Сложность алгоритма

Время работы алгоритма равно времени работы алгоритма $F2 \mid \mid C_{max}$.

Сложность алгоритма $O(n\log n)$.