К-d деревья и перечисление точек в произвольном прямоугольнике (статика)

Материал из Викиконспекты
Перейти к: навигация, поиск
Конспект готов к прочтению.

Определение и построение

Пример

K-d дерево (short for k-dimensional tree) — статическая структура данных для хранения точек в [math]k[/math]-мерном пространстве. Позволяет отвечать на запрос, какие точки лежат в данном прямоугольнике.

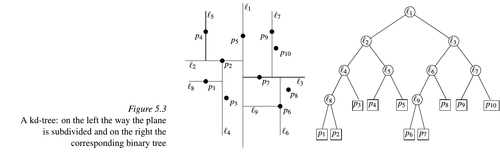
Строится это дерево следующим образом: разобьём все точки вертикальной прямой так, чтобы слева (нестрого) и справа (строго) от неё было примерно поровну точек (для этого посчитаем медиану первых координат). Получим подмножества для левого и правого ребёнка. Далее построим для этих подмножеств деревья, но разбивать будем уже не вертикальной, а горизонтальной прямой (для этого посчитаем медиану вторых координат). И так далее (раз считаем, что [math]k = 2[/math], то на следующем уровне вновь будем разбивать вертикальными прямыми).

Замечание: проблемы могут возникнуть, если много точек имеют одинаковую координату, тогда разбить примерно поровну не получится (почти все точки будут лежать на медиане и попадут в левую часть). Лучший способ борьбы с этим — не вспоминать о данной проблеме совсем. Но вообще с этим борются, используя composite numbers, то есть сравнивая ещё и по другой (другим) координате.

Реализовывать построение можно рекурсивно с помощью функции [math]BuildKdTree(P, Depth)[/math], принимающей множество точек и глубину. В зависимости от остатка при делении на размерность (рассмотрим [math] k = 2 [/math], в таком случае от чётности размерности) сплитим множество на два подмножества и делаем рекурсивные вызовы. Для лучшего понимания приведём псевдокод: 

BuildKdTree(P, Depth)
//Input. A set of points P and the current depth Depth.
//Output. The root of a kd-tree storing P.
if P contains only one point
   return a leaf storing this point
else if depth is even
   Split P into two subsets [math]P_1[/math] and [math]P_2[/math] with a vertical line [math]l[/math] through the median x-coordinate of the points in P
else 
   Split P into two subsets [math]P_1[/math] and [math]P_2[/math] with a horizontal line [math]l[/math] through the median y-coordinate of the points in P. 
[math]V_{left}[/math] <- BuildKdTree([math]P_1[/math], Depth + 1)
[math]V_{right}[/math] <- BuildKdTree([math]P_2[/math], Depth + 1)
Create a node v storing [math]l[/math], make [math]V_{left}[/math] the left child of v, and make [math]V_{right}[/math] the right child of v.
return v

Лемма (О времени построения):
Построение выполняется за [math]O(n \log n)[/math].
Доказательство:
[math]\triangleright[/math]

Время построения обозначим [math]T(n)[/math]. Поиск медианы можно сделать за линейное время, поэтому достаточно очевидно, что:

[math]T(n) = O(1)[/math] if [math]n = 1[/math].

[math]T(n) = O(n) + 2 \cdot T(n / 2)[/math], otherwise.

Умные люди могут сразу же заметить, что решением этого является [math]T(n) = O(n \log n)[/math]. А люди моего уровня могут почитать умные книжки или просто поверить в данный факт. Хотя могу неформально пояснить: второе слагаемое даёт [math]O(n)[/math] суммарно, а всего слагаемых из-за неё получится [math]O(\log n)[/math]. То есть получим [math]O(n)[/math] из-за второго слагаемого и ещё [math]O(\log n)[/math] слагаемых вида [math]O(n)[/math].

Также стоит отметить, что можно и не искать медиану за линейное время, а просто посортить все точки в самом начале и дальше использовать это. В реализации попроще, асимптотика та же.
[math]\triangleleft[/math]
Лемма (О занимаемой памяти):
K-d дерево требует [math]O(n)[/math] памяти.
Доказательство:
[math]\triangleright[/math]
Высота дерева, очевидно, логарифмическая, а листьев всего [math]O(n)[/math]. Поэтому будет [math]O(n)[/math] вершин, каждая занимает [math]O(1)[/math] памяти.
[math]\triangleleft[/math]

By the way, если считать [math]k[/math] константой, то и для случая большей размерности эти оценки будут такими же (доказывается аналогично).

Запрос

Пусть нам поступил какой-то прямоугольник [math]R[/math]. Нужно вернуть все точки, которые в нём лежат. Будем это делать рекурсивно, получая на вход корень дерева и сам прямоугольник [math]R[/math]. Обозначим область, соответствующую вершине [math]v[/math], как [math]region(v)[/math]. Она будет прямоугольником, одна или более границ которого могут быть на бесконечности. [math]region(v)[/math] можно явно хранить в узлах, записав при построении, или же считать при рекурсивном спуске. Если корень дерева является листом, то просто проверяем одну точку и при необходимости репортим её. Если нет, то смотрим пересекают ли регионы детей прямоугольник [math]R[/math]. Если да, то запускаемся рекурсивно от такого ребёнка. При этом, если регион полностью содержится в [math]R[/math], то можно репортить сразу все точки из него. Тем самым мы, очевидно, вернём все нужные точки и только их. Чтобы стало совсем понятно, приведём псевдокод: 

SearchKdTree(v, R)
//Input. The root of (a subtree of) a kd-tree, and a range R.
//Output. All points at leaves below v that lie in the range.
if v is a leaf 
   Report the point stored at v if it lies in R.
else 
   if region(v.left) is fully contained in R
      ReportSubtree(v.left)
   else if region(v.left) intersects R
      SearchKdTree(v.left, R)
   if region(v.right) is fully contained in R
      ReportSubtree(v.right)
   else if region(v.right) intersects R
      SearchKdTree(v.right, R)

Здесь [math]ReportSubtree[/math] репортит все точки в поддереве.

By the way, точно так же можно перечислять точки в любом множестве, ведь нигде не используется, что [math]R[/math] — прямоугольник.

Теорема (О времени на запрос):
Перечисление точек в прямоугольнике выполняется за [math]O(\sqrt n + ans)[/math], где [math]ans[/math] — размер ответа.
Доказательство:
[math]\triangleright[/math]

Сперва заметим, что все [math]ReportSubtree[/math] суммарно выполняются за [math]O(ans)[/math]. Поэтому достаточно доказать оценку для числа рекурсивных вызовов. А рекурсивные вызовы выполняются только для тех вершин, регионы которых пересекают [math]R[/math], но не содержатся в нём. Такие регионы обязательно пересекают хотя бы одну (axis-parallel) сторону заданного прямоугольника. Оценим количество регионов, которые могут пересекаться произвольной вертикальной прямой. Для горизонтальной прямой это будет аналогично.

Обозначим максимально возможное количество регионов, пересекаемых какой-либо вертикальной прямой, в дереве для [math]n[/math] точек, у которого первое разбиение делается вертикальной прямой, как [math]Q(n)[/math]. Рассмотрим произвольную вертикальную прямую [math]l[/math]. Она будет пересекать регион корня и какого-то одного из его детей (например, левого). При этом ни один из регионов в другом (правом) поддереве пересекать она не может. Левая половина разбита ещё на 2 части горизонтальной прямой, в каждой из них примерно [math]n / 4[/math] вершин, и они хранятся в поддереве, у которого первое разбиение делается вертикальной прямой. Это даёт нам следующее соотношение:

[math]Q(n) = O(1)[/math] if [math]n = 1[/math].

[math]Q(n) = 2 + 2 \cdot Q(n / 4)[/math], otherwise.

Нетрудно заметить, что [math]Q(n) = O(\sqrt n)[/math] является решением. Принимая во внимание всё, что писалось выше, получаем требуемое.
[math]\triangleleft[/math]

By the way, в общем случае время на запрос [math]O(n^{1 - 1/k} + ans)[/math]. Быстренько прикинув, я получил соотношение [math]Q(n) = k + 2^{k - 1} \cdot Q(n / 2^k)[/math]. Кажется, так и есть, но это не особо надо, просто пусть будет, полезно же.

Ссылки

Источник — «http://neerc.ifmo.ru/wiki/index.php?title=К-d_деревья_и_перечисление_точек_в_произвольном_прямоугольнике_(статика)&oldid=36174»