Персистентный стек
Эффективная реализация
Попробуем решить задачу эффективнее. Заведем массив запросов, модифицирующих стек.
У каждого элемента массива будет 2 поля: значение в вершине стека и индекс предыдущей версии стека.
Тогда операции push и pop будут иметь следующий вид:
- — добавляет элемент х в стек с номером i, результирующий стек будет иметь номер .
function push(i : uint, x : T): s.top = s.top + 1 s[s.top].value = x s[s.top].prev = i
- — возвращает значение, хранящееся в элементе с номером i и копирует элемент, предыдущий для него.
результирующий стек будет иметь номер .
T pop(i : uint): T k = s[i] k = s[k.prev] push(k.prev, k.value)
Пример
- Пусть изначально у нас есть один пустой стек. Запишем его в массив.
| index | 1 |
|---|---|
| value | |
| prev |
- Далее выполним . Создается новая вершина со значением 3, ссылающаяся на 1-ую, помещаем ее во 2-ую ячейку массива:
| index | 1 | 2 |
|---|---|---|
| value | 3 | |
| prev | 1 |
- Аналогично выполним :
| index | 1 | 2 | 3 |
|---|---|---|---|
| value | 3 | 5 | |
| prev | 1 | 2 |
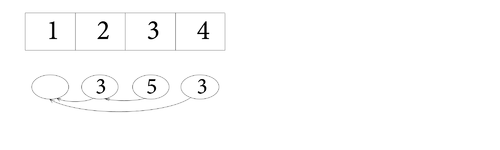
- Выполним . он возвращает 5 и копирует 2-ую вершину.
| index | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| value | 3 | 5 | 3 | |
| prev | 1 | 2 | 1 |
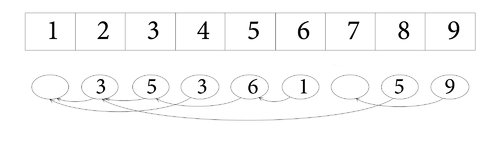
- Так будет выглядеть массив после последовательности операций
| index | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| value | 3 | 5 | 3 | 6 | 1 | 5 | 9 | ||
| prev | 1 | 2 | 1 | 3 | 5 | 2 | 7 |
В итоге мы имеем доступ ко всем версиям стека за времени и памяти.