Матрица смежности графа
Версия от 17:24, 6 ноября 2015; Lapenok.aleksej (обсуждение | вклад) (→Оценка памяти и времени работы)
| Определение: |
| Матрицей смежности (англ. Adjacency matrix) невзвешенного графа называется матрица , в которой — количество рёбер, соединяющих вершины и , причём при каждую петлю учитываем дважды, если граф не является ориентированным, и один раз, если граф ориентирован. |
| Определение: |
| Матрицей смежности (англ. Adjacency matrix) взвешенного графа называется матрица , в которой — вес ребра, соединяющего вершины и . |
Примеры матриц смежности:
| Взвешенность графа | Вид графа | Матрица смежности |
|---|---|---|
| Не взвешенный граф | 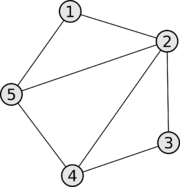
|
|
| Взвешенный граф | 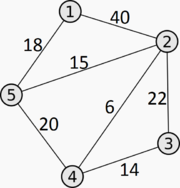
|
Оценка памяти и времени работы
Матрица смежности занимает памяти. За можно определить вес ребра или его наличие между любыми двумя вершинами. Такой способ хранения графа хорошо подходит для плотных графов, в которых число рёбер между различными парами вершин .
Свойства
| Утверждение: |
Для графов без петель и кратных рёбер матрица смежности бинарна (состоит из нулей и единиц). |
| Утверждение: |
Для графов без петель и кратных рёбер главная диагональ матрицы смежности целиком состоит из нулей. |
| Утверждение (о сумме элементов строки матрицы смежности для ориентированного графа): |
Сумма элементов -й строки равна , то есть .
Аналогично сумма элементов -го стоблца равна , то есть . |
| Утверждение (о сумме элементов строки матрицы смежности для неориентированного графа): |
Матрица смежности является симметричной. |
| Сумма элементов -й строки равна , то есть . Вследствие симметричности суммы элементов -й строки и -го столбца равны. |
| Теорема (о поиске количества путей заданной длины с помощью матрицы смежности ориентированного графа): |
Пусть — матрица смежности ориентированного графа без петель и , где . Тогда равно количеству путей длины . |
| Доказательство: |
|
Утверждение очевидно при . Пусть , и утверждение верно для . Тогда , где равно количеству путей длины . Следовательно, |
См. также
Источники информации
- Харари Фрэнк Теория графов Пер. с англ. и предисл. В. П. Козырева. Под ред. Г.П.Гаврилова. Изд. 2-е. — М.: Едиториал УРСС, 2003. — 296 с. — ISBN 5-354-00301-6
- Асанов М. О., Баранский В. А., Расин В. В. Дискретная математика: графы, матроиды, алгоритмы — НИЦ РХД, 2001. — 288 с. — ISBN 5-93972-076-5