Род, толщина, крупность, число скрещиваний
Версия от 00:40, 5 января 2016; Конспектор (обсуждение | вклад)
| Определение: |
| Родом графа называется наименьшее число ручек, которые нужно добавить к сфере, чтобы уложить . |
| Определение: |
| Толщиной (англ. thickness) графа называется наименьшее число планарных графов, объединение которых есть . |
| Определение: |
| Крупностью графа называется наибольшее число непланарных графов в , не пересекающихся по рёбрам. |
| Определение: |
| Числом скрещиваний (англ. crossing number) графа называется число пересечений рёбер, которое должно быть при расположении на плоскости. |
Содержание
Укладка графа на ориентируемой поверхности
| Утверждение: |
Любой граф можно уложить на некоторой ориентируемой поверхности. |
| Это лекго понять, если нарисовать произвольный граф на плоскости, причём некоторые рёбра могут пересекаться, и для каждомого пересечении рёбер добавить к плоскости ручку; затем провести одно ребро по ручке, другое — под ней. |
Укладка графа на сфере
| Утверждение: |
Любой планарный граф можно уложить на сфере. |
| Положим сферу на плоскость так, чтобы точка касания сферы плоскости не пренадлежала графу. Проведём линии, соединяющие вершины графа с центром сферы. Точки пересечений линий со сферой будут вершинами графа на сфере. Таким образом мы получили однозначное соответствие точек сферы и точек плоскости, значит планарный граф можно уложить на сфере, так как каждой точке сферы (кроме точки, противоположной точки касания сферы плоскости) соответствует одна точка плоскости. |
Укладка графа на торе
| Определение: |
| Если граф можно уложить на торе, то он тороидальный. |
| Утверждение: |
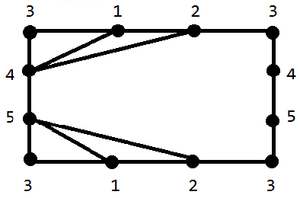
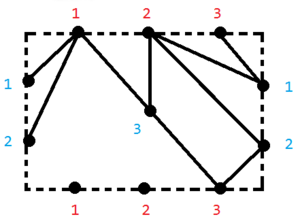
и являются тороидальными. |
|
Укладки графа на торе представлены на рисунках. |
См. также
Источники информации
- Харари Фрэнк Теория графов Пер. с англ. и предисл. В. П. Козырева. Под ред. Г.П.Гаврилова. Изд. 2-е. — М.: Едиториал УРСС, 2003. — 296 с. — ISBN 5-354-00301-6
- Википедия — Толщина графа
- Wikipedia — Crossing number