Совершенное паросочетание в кубическом графе

Материал из Викиконспекты
Версия от 18:54, 28 января 2016; Profick (обсуждение | вклад) (→‎Время работы)
Перейти к: навигация, поиск

Теорема Петерсона (Petersen)

Теорема (Петерсон):
Кубический граф, у которого нет совершенного паросочетания, содержит как минимум [math]3[/math] моста.

Следствие из данной теоремы: для любого двусвязного кубического графа существует совершенное паросочетание.

Теорема Фринка (Frink)

Теорема (Фринк):
Пусть [math]G(V, E)[/math] — двусвязный кубический граф.

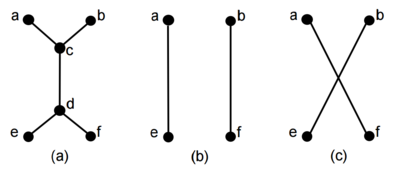
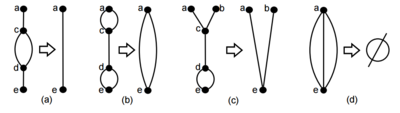
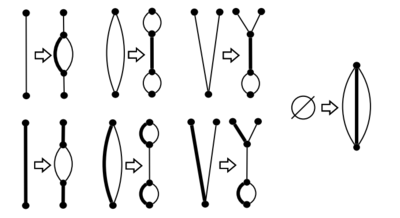
Возьмём ребро [math]p = (c, d)[/math]. Пусть вершины [math]a[/math] и [math]b[/math] смежены с вершиной [math]c[/math], а вершины [math]e[/math] и [math]f[/math] смежны с вершиной [math]d[/math] (рисунок [math]1 (a)[/math]).

Как минимум одно из двух сокращений графа [math]G[/math], состоящее из удаления вершин [math]c, d[/math] и пересоединения вершин [math]a, b, e, f[/math] рёбрами [math](a, e), (b, f)[/math] или [math](a, f), (b, e)[/math] (рисунок [math]1 (b), (c)[/math]) сохранит двусвязность графа.
Доказательство:
[math]\triangleright[/math]

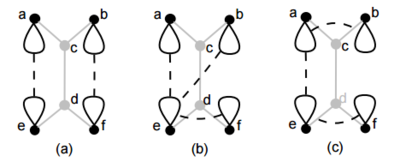
Обозначим компоненты графа [math]G(V - {c, d})[/math] как [math]A, B, E, F[/math], которые содержат вершины [math]a, b, e, f[/math] соответственно. Так как [math]G[/math] не имеет мостов (соответственно [math]p[/math] не является мостом) должно существовать ребро, соединяющее одну из компонент [math]A[/math] или [math]B[/math], с одной из компонент [math]E[/math] или [math]F[/math]. Без потери общности предположим, что [math]A[/math] соединено с [math]E[/math]. Заметим, что рёбра [math](b, c), (d, f)[/math] так же не являются мостами, значит возможны три случая (с учётом изоморфизма) (рисунок [math]3[/math]):

  • компонента [math]B[/math] соединена с [math]F[/math]
  • компонента [math]B[/math] соединена с [math]E[/math] и компонента [math]E[/math] соединена с [math]F[/math]
  • компонента [math]A[/math] соединена с [math]B[/math] и компонента [math]E[/math] соединена с [math]F[/math]

Во всех трёх случаях если [math]G(V - {c, d})[/math] расширить рёбрами [math](a, f), (b, e)[/math] (получим граф [math]G'[/math]), добавленные рёбра будут лежать на некотором цикле в [math]G'[/math] (рисунок [math]4[/math]). Так же, для любой пары вершин [math]u, v[/math] [math]\in[/math] [math]{a, b, e, f}[/math] существует цикл в [math]G'[/math], содержащий данные вершины. Чтобы доказать, что [math]G'[/math] двусвязен, нужно показать, что каждое ребро [math]r[/math] из [math]G'[/math] лежит на некотором цикле в [math]G'[/math]. Пусть цикл [math]C[/math] в [math]G[/math] содержит [math]r[/math] (такой цикл существует, так как [math]G[/math] двусвязен). Если [math]C[/math] не проходит через вершины [math]c, d[/math] тогда [math]C[/math] так же является циклом в [math]G'[/math], иначе построим цикл [math]C'[/math] графа [math]G'[/math] из [math]C[/math] следующим образом:

  • если путь [math] x - c - d - y [/math] [math]\in[/math] [math] C [/math], [math] x [/math] [math]\in[/math] [math] \{a, b\} [/math], [math] y [/math] [math]\in[/math] [math] \{e, f\} [/math], удалим этот путь и добавим любой другой из [math] x [/math] в [math] y [/math] в [math] G' [/math], не содержащий [math]r[/math] (такой путь всегда существует, так как [math] x [/math] и [math] y [/math] принадлежат некоторому циклу в [math] G' [/math]),
  • если путь [math] a - c - b [/math] [math]\in[/math] [math] C [/math], удалим этот путь и добавим любой другой из [math] a [/math] в [math] b [/math] в [math] G' [/math], не содержащий [math]r[/math],
  • если путь [math] e - d - f [/math] [math]\in[/math] [math] C [/math], удалим этот путь и добавим любой другой из [math] e [/math] в [math] f [/math] в [math] G' [/math], не содержащий [math]r[/math].
[math]C'[/math] это набор циклов (так как [math]C'[/math] получен из [math]C[/math] путём преобразования некоторых путей) и содержит [math]r[/math]. Из этого следует, что каждое ребро графа [math]G'[/math] лежит на некотором цикле, то есть граф не содержит мостов. Значит [math]G'[/math] двусвязен.
[math]\triangleleft[/math]
Рисунок 1.
Рисунок 2.
Рисунок 3.
Рисунок 4.


Алгоритм поиска совершенного паросочетания за O(n^2) (Frink's algorithm)

  • будем сокращать данный граф [math]G[/math] вышеизложенным способом (на каждой итерации можем выбирать любое ребро) пока не удалим все вершины,
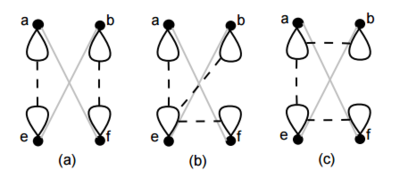
  • когда все вершины закончились, создадим пустое совершенное паросочетание [math]M[/math] и начнём обратный процесс для всех сокращений, то есть восстановление графа (начиная с последних удалённых вершин). Каждый такой шаг будет приводить к одному из четырёх базовых случаев, представленных в рисунке [math]5[/math] или к одному из специальных случаев из рисунка [math]6[/math]. Восстановление для всех специальных случаев, а так же для первых трёх базовых выполняется по строгому алгоритму, т.е. разрешим за [math]O(1)[/math]. Единственный проблемный случай, когда оба ребра принадлежат совершенному паросочетанию. В этой ситуации необходимо найти альтернативный цикл, содержащий как минимум одно из этих рёбер и обновить паросочетание с этим циклом. Эти действия сводят четвёртый базовый случай к одному из первых трёх.


Рисунок 5.
Рисунок 6.

Реализация алгоритма Фринка

  • [math]G[/math] двусвязный кубический граф,
  • [math]M[/math] совершенное паросочетание [math]G[/math].
  • функция [math]bridgeless[/math] сообщает, имеет ли граф мост.
  • функция [math]alternating\_cycle[/math] принимает три параметра: граф, совершенное паросочетание и ребро. Возвращает альтернативный цикл, включающий в себя данное ребро и обновляет совершенное паросочетание.
  • функции [math]reductions[/math] и [math]simple\_reversion[/math] сокращают и восстанавливают граф соответственно.
if [math]|V| = 0[/math] then
    return [math]\varnothing[/math]
else
    [math]v - w = E[0][/math]
    [math]R = reductions(G, v - w)[/math]
    if [math] bridgeless(G[V − {v, w}, E \cup R[0]])[/math] then
        [math]r = R[0][/math]
    else
        [math]r = R[1][/math]
    end if
    [math]M \leftarrow frink\_matching(G[V - \{v, w\}, E \cup r])[/math]
    if [math]|r \cap M| = 2 [/math] then
        [math]C \leftarrow alternating\_cycle(G, M, r[0])[/math]
        [math]M \leftarrow M \oplus C[/math]
    end if
    [math]M \leftarrow (M - r) \cup simple\_reversion(G, v, w, r, M)[/math]
    return [math]M[/math]
end if

Время работы алгоритма Фринка

Операция сокращения должна на каждом шаге проверять граф на наличие мостов[math]O(n)[/math], кроме того, при возникновении четвёртого базового случая требуется найти альтернативный цикл за [math]O(n)[/math]. В алгоритме [math]O(n)[/math] операций сокращения и восстановления графа, причем каждая из этих операций требует [math]O(n)[/math] времени. Таким образом, весь этот алгоритм исполняется за время [math]O(n^2)[/math].

Ссылки

Источники информации

Источник — «http://neerc.ifmo.ru/wiki/index.php?title=Совершенное_паросочетание_в_кубическом_графе&oldid=51994»