PpmtnCmax
Версия от 06:05, 8 июня 2016; Веда (обсуждение | вклад) (Новая страница: «{{Задача |definition = Имеется <tex>M</tex> однородных машин, работающих параллельно. Есть <tex>n</tex> ра...»)
| Задача: |
| Имеется однородных машин, работающих параллельно. Есть работ, каждая из которых имеет своё время окончания . Работа может быть прервана и продолжена позже. Необходимо составить такое расписание, чтобы значение было минимальным. |
Алгоритм
Будет строить расписание по нижней оценке.
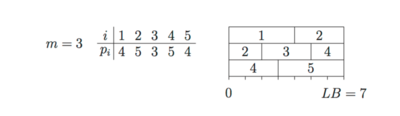
Мы не сможем выполнить работы быстрее, чем , так как работы на разных станках не могут выполняться в один момент времени. И нам потребуется минимум времени, чтобы выполнить все работы, используя ресурсы только станков.
Обозначим нижнюю оценку как .
Расписание, удовлетворяющее этой оценке может быть построено за .
Будем выполнять работы на станке в произвольном порядке до тех пор, пока не будет достигнуто время . Тогда оставшаяся часть работы, которая не была закончена, переносится в начало следующего станка. Таким образом, времена выполнения одной работы на разных станках не будут совпадать.
Источники информации
- Peter Brucker. «Scheduling Algorithms» — «Springer», 2006 г. — 108 стр. — ISBN 978-3-540-69515-8