Использование обхода в глубину для поиска точек сочленения

Материал из Викиконспекты
Перейти к: навигация, поиск

Дан связный неориентированный граф [math] G [/math]. Найти все точки сочленения в [math] G [/math] за время [math] O(|V| + |E|)[/math]

Алгоритм

Теорема:
Пусть [math]T[/math] — дерево обхода в глубину, [math]root[/math] — корень [math]T[/math]. Вершина [math]u \ne root[/math] — точка сочленения [math]\Leftrightarrow \exists v \in T[/math] — сын [math]u[/math] : из [math]v[/math] или любого потомка вершины [math]v[/math] нет обратного ребра в предка вершины [math]u[/math]. [math]root[/math] — точка сочленения [math]\Leftrightarrow root[/math] имеет хотя бы двух сыновей в дереве поиска в глубину.
Доказательство:
[math]\triangleright[/math]
Рисунок к [math]\Leftarrow[/math]

[math]\Leftarrow[/math]

  1. Удалим [math]u[/math] из [math]G[/math]. Докажем, что не существует пути из [math]v[/math] в любого предка вершины [math]u[/math]. Пусть это не так. Тогда [math]\exists x \in T[/math] — предок [math]u[/math] : [math]\exists[/math] путь из [math]v[/math] в [math]x[/math] в [math]G \backslash u[/math]. Пусть [math]w[/math] — предпоследняя вершина на этом пути, [math]w[/math] — потомок [math]v[/math]. [math](w, x)[/math] — не ребро дерева [math]T[/math](в силу единственности пути в дереве) [math]\Rightarrow (w, x)[/math] — обратное ребро, что противоречит условию.
  2. Пусть у [math]root[/math] хотя бы два сына. Тогда при удалении [math]root[/math] не существует пути между его поддеревьями, так как не существует перекрестных ребер [math]\Rightarrow root[/math] — точка сочленения.


[math]\Rightarrow[/math]

  1. Докажем что из отрицания второго утверждения следует отрицание первого. Обозначим через [math]G'[/math] граф, состоящий из вершин, не являющихся потомками [math]u[/math]. Удалим вершину [math]u[/math]. Очевидно, что граф [math]G'[/math] и все поддеревья вершины [math]u[/math] останутся связными, кроме того из каждого поддерева есть ребро в [math]G' \Rightarrow G \backslash u[/math] — связный [math]\Rightarrow u[/math] — не точка сочленения.
  2. Пусть [math]root[/math] — точка сочленения и у него есть только один сын. Тогда при удалении [math]root[/math] остается дерево с корнем в его сыне, содержащее все остальные вершины графа, то есть оставшийся граф связен — противоречие с тем, что [math]root[/math] — точка сочленения.
[math]\triangleleft[/math]


Красным цветом обозначены точки сочленения
Синим — ребра по которым идет DFS

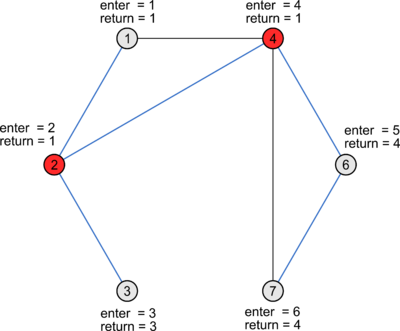
Пусть [math]tin[u][/math] — время входа поиска в глубину в вершину [math]u[/math]. Через [math]up[u][/math] обозначим минимум из времени захода в саму вершину [math]tin[u][/math], времен захода в каждую из вершин [math]p[/math], являющуюся концом некоторого обратного ребра [math](u,p)[/math], а также из всех значений [math]up[v][/math] для каждой вершины [math]v[/math], являющейся непосредственным сыном [math]u[/math] в дереве поиска.

Тогда из вершины [math]u[/math] или её потомка есть обратное ребро в её предка [math]\Leftrightarrow \exists[/math] такой сын [math]v[/math], что [math]up[v] \lt tin[u][/math].

Таким образом, если для текущей вершины [math]v \ne root [/math] существует непосредственный сын [math]v[/math]: [math]up[v] \ge tin[u][/math], то вершина [math]u[/math] является точкой сочленения, в противном случае она точкой сочленения не является.


Реализация

function findCutPoints(G[n]: Graph): // функция принимает граф G с количеством вершин n и выполняет поиск точек сочленения  во всем графе 
    visited = array[n, false]
                   
   function dfs(v: int, p: int):
      time = time + 1
      up[v] = tin[v] = time 
      visited[v] = true             
      for u: (v, u) in G   
         if u == p
            continue
         if visited[u] == true
            up[v] = min(up[v], tin[u])
         else
            dfs(u, v) 
            up[v] = min(up[v], tin[u])
            if up[to] >= tin[v] && p != -1 //если граф состоит из 2 вершин и одного ребра, то p != -1 спасёт, иначе выведет 1 точку сочленения 
                 v — cutpoint 
      if v — root
            v — cutpoint 
                   	   
   for i = 1 to n             
      if visited[i] == false                
         dfs(i, -1)

См. также

Источники информации

Источник — «http://neerc.ifmo.ru/wiki/index.php?title=Использование_обхода_в_глубину_для_поиска_точек_сочленения&oldid=59273»