Квантовые алгоритмы
| Определение: |
| Квантовый алгоритм (англ. quantum algorithm) представляет собой классический алгоритм, который задает последовательность унитарных операций (гейтов, или вентилей) с указанием, над какими именно кубитами[1] их надо совершать. |
Содержание
Алгоритм проверки чётности
Постановка задачи
| Задача: |
| Пусть имеется функция , такая, что с неизвестным . Найти за минимальное количество обращений к функции . |
Пример:
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
Реализация
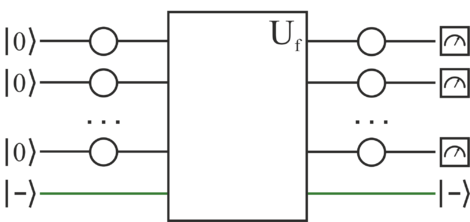
Для начала инициализируем начальные кубитов состоянием ноль. Проводим их всех через гейт Адамара (англ. Hadamard gate) и получаем все возможные суперпозиции. Суперпозиции передаём в "черный ящик", который реализован в виде вентиля . Сам результат опять пропускаем через гейт Адамара. В конце измеряем результат, который будет являться искомой .
В качестве бита, который будет содержать ответ, будет использоваться суперпозиция:
Выразим неизвестную:
Сложность
Классический алгоритм: .
Квантовый алгоритм: . Такая сложность достигается благодаря квантовым свойства[2], а конкретно параллелизму[3].
Алгоритм Саймона
Постановка задачи
| Задача: |
| Пусть имеется функция , такая, что с неизвестным . Найти за минимальное количество обращений к функции . |
Пример:
| 000 | 010 | 001 | 100 | 010 | 000 | 100 | 001 |
Реализация
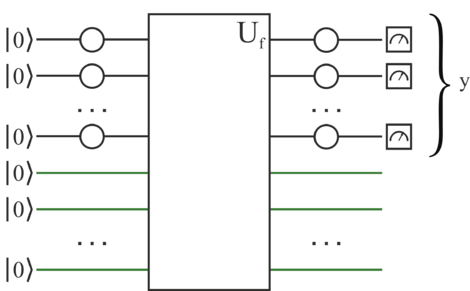
Задача похожа на задачу нахождения коллизии, так как необходимо найти два значения, при которых их выходные значения будет одинаковыми, затем вычислить между ними разницу, которая и будет ответом задачи.
Аналогично предыдущему алгоритму вычисляем результат, который будет являться некоторой строкой, дающей при скалярном умножении на искомую ноль. После итерации алгоритма получим систему из линейных уравнений; решив эту систему уравнений, найдём искомую .
Особенности алгоритма:
- для решения СЛАУ [4] необходим препроцессинг на классическом компьютере;
- алгоритм может допускать ошибку(возможно, какие-то уравнения не будут линейно независимыми и система не будет иметь решений) с вероятностью при одном цикле прохода алгоритма. Этого можно избежать, если прогнать алгоритм несколько раз, так для раз, вероятность будет равна: . Например, при вероятность будет .
Сложность
Классический алгоритм: .
Квантовый алгоритм: .
Алгоритм нахождения периода
Постановка задачи
| Задача: |
| Пусть имеется функция , такая, что с неизвестным периодом . Найти за минимальное количество обращений к функции . |
Перефразируем задачу: у нас есть периодичная функция, для которой необходимо найти её период, путём нахождения коллизии.
Реализация
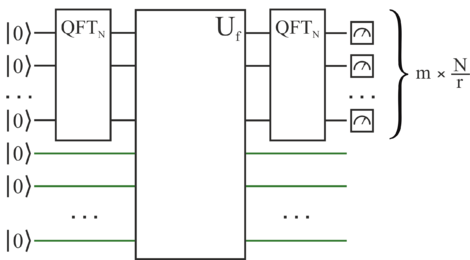
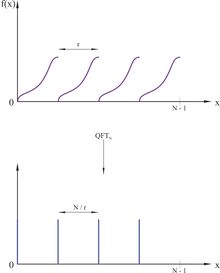
Чтобы решить задачу, воспользуемся квантовым преобразованием Фурье[5](англ. Quantum Fourier transform; далее QFT). QFT — гейт, который реализует матрицу дискретного преобразования Фурье[6] над квантовым состоянием. Идея в следующем: есть периодическая функция с периодом , после QFT, получим новую периодическую функцию с периодом , где — модуль, с которым мы работаем.
, где
Так аналогично предыдущему алгоритму, но пользуясь QFT, получаем результат . Выполнив данный алгоритм раз, найдём наибольший общий делитель[7] от полученных чисел, который, с некоторой вероятностью, будет искомым периодом , при этом вероятность ошибки будет экспоненциально падать с каждой попыткой.
Примечание: Алгоритм нахождения периода используется в алгоритме Шора[8], который позволяет решать задачу факторизации числа.
Сложность
Классический алгоритм: .
Квантовый алгоритм: .
См.также
- Квантовые гейты
- Алгоритм Гровера
- Алгоритм Шора
- Веб-приложение, использующее WebGL, чтобы имитировать до 22 кубитов на GPU
- Веб-приложение, для написания и визуализации квантовых алгоритмов
- Языки программирования для квантового компьютера
Примечания
- ↑ Википедия — Кубит
- ↑ Википедия — Квантовый компьютер
- ↑ Википедия — Квантовый параллелизм
- ↑ Википедия — Система линейных алгебраических уравнений
- ↑ Wikipedia — Quantum Fourier transform
- ↑ Википедия — Дискретное преобразование Фурье
- ↑ Википедия — Наибольший общий делитель
- ↑ Wikipedia — Shor's algorithm