Поиск ближайших соседей с помощью иерархического маленького мира
Иерархия навигируемых малых миров (англ. Hierarchical Navigable Small World) — структура данных, позволяющая эффективно находить K почти что ближайших соседей. По своей концепции напоминает список с пропусками.
Маленький мир
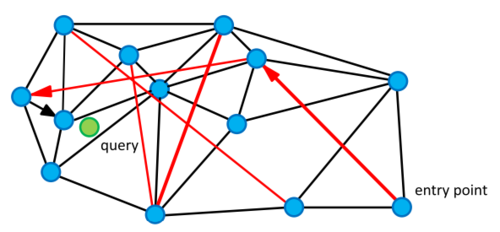
Маленький мир (англ. Small World) — граф, в котором мат. ожидание кратчайшего пути между двумя случайно выбранными вершинами растёт пропорционально . Но при этом средняя степень вершины мала.
Для маленького мира на точках в Евклидовом пространстве, приближенный поиск K ближайших соседей будет выглядеть так:
KNN(request, m, k):
nearest = new TreeSet() // вершины упорядочены по возрастанию расстояния до request
candidates = new TreeSet()
visited = new HashSet()
for i = 1 to m
candidates.add(случайная вершина графа)
tempNearest = new TreeMap()
while true
current = candidates.popMin()
if current дальше чем k-й элемент nearest
break
for v : смежные с current вершины
if !visited.contains(v)
candidates.add(v)
visited.add(v)
tempNearest.add(v)
nearest.addAll(tempNearest)
return k первых вершин из nearest
Очевидный недостаток этого алгоритма — опасность свалиться в локальный минимум.
Описание структуры
Иерархический Маленький мир (англ. Hierarchical Navigable Small World) — слоистая структура графов. На нулевом слое представлены все N вершин из исходной выборки. Вершина, присутствующая на уровне L так же присутствует на уровне L + 1 с вероятностью P. Т.е. кол-во слоёв растет как . Количество соседей каждой вершины на каждом уровне ограниченно константой, что позволяет делать запросы на добавление и удаление вершины за
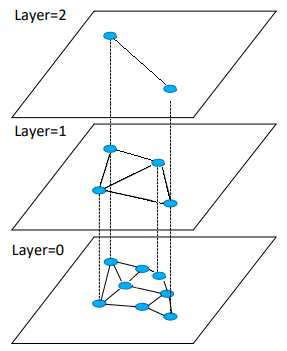 Иерархический маленький мир. Источник |
Операции над структурой
Поиск ближайших соседей в слое
Жадно идём по уровню в сторону запроса.
SearchLayer(q, ep, ef, lc):
// Ввод: запрос q, входная точка ep, количество ближайших соседей q ef, номер слоя lc
// Вывод: ef ближайших соседей q
candidates = new TreeSet() // вершины упорядочены по возрастанию расстояния до request
result = new TreeSet()
visited = new HashSet()
while candidates.isNotEmpty()
current = candidates.getMin()
furthest = result.getMax()
if distance(current, q) > distance(furthest, q)
break // мы в локальном минимуме, все остальные вершины в кандидатах ещё дальше.
for v : смежные с current вершины
if !visited.contains(r)
visited.add(v)
furthest = result.getMax()
if distance(v, q) < distance(furthest, q) or result.count() < ef
candidates.add(v)
result.add(v)
if result.count() > ef
result.removeLast()
return result