Ядро
Ядерный трюк (англ. kernel function) метод в машинном обучении, позволяющий перевести элементы для случая линейной неразделимости в новое линейно разделимое пространство. Такое пространство называют спрямляющим. Поскольку для любой непротиворечивой выборки соответствующее пространство большей размерности существует, главной проблемой становится его найти.
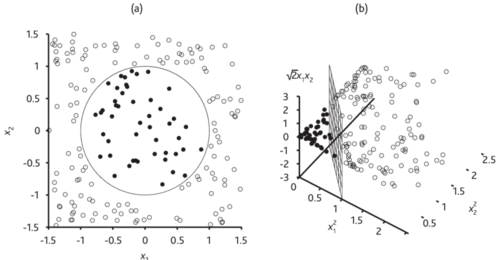
Пример: На первой картинке справа можно увидеть, что 2 класса не разделимы линейно, но после преобразования появляется разделяющая плоскость.
Описание
| Определение: |
| Функция $K(x,x'):X×X\rightarrow \mathbb{R}$ называется ядром (англ. kernel), если она может быть представлена в виде $K(x,x')=\langle \varphi(x),\varphi(x')\rangle_H$ при некотором отображении $\varphi(x):X\rightarrow H$, где $H$ — пространство со скалярным произведением. |
Поскольку для задачи линейного разделения объектов не требуется их признаковое описание, а достаточно скаляров, то можно заменить скалярное произведение $\langle x,x'\rangle$ на ядро $K(x,x')$. Более того, можно вообще не строить спрямляющее пространство $H$ в явном виде, и вместо подбора отображения $\varphi$ заниматься непосредственно подбором ядра.
Можно пойти ещё дальше, и вовсе отказаться от признаковых описаний объектов. Во многих практических задачах объекты изначально задаются информацией об их попарном взаимоотношении, например, отношении сходства. Если эта информация допускает представление в виде двуместной функции $K(x,x')$, удовлетворяющей аксиомам скалярного произведения, то задача может решаться методом опорных векторов.
Преимущества и недостатки
Преимущества
- Обобщение линейных методов на нелинейный случай:
а) с сохранением вычислительной эффективности линейных методов.
б) с сохранением преимуществ линейных методов (локальный оптимум является глобальным, нет локальных оптимумов=>меньше переобучение).
- Объекты для которых не существует векторных представлений фиксированной длины.
- Ускоренное вычисление скалярных произведений для высоких значений размерностей.
Недостатки
- Вычислительно сложно проверять принадлежность функции ядру.
- Поиск подходящего ядра экспоненциально сложен из-за их большого многообразия.
Характерные случаи применения
- Признаковое пространство высокой размерности.
Например все полиномы до степени $M$, для случая Гаусовского ядра — признаковое пространство бесконечной размерности.
- Случай, когда сложно представить объекты векторами фиксированной длины.
Такие, как строки, множества, картинки, тексты, графы, 3D-структуры и т.д.
- Существование естественного определения скалярного произведения.
Такие, как строки (число совместно встречающихся подстрок) или множества (напр. для множеств $S_1$ и $S_2$ ядром будет являться $K(S_1, S_2) = 2^{|S_1\cap S_2|}$).
- Скалярное произведение может быть подсчитано эффективно.
Выбор функции ядра
| Теорема (Мерсера): |
Функция $K(x,y)$ является ядром тогда и только тогда, когда она симметрична: $K(x,y)=K(y,x)$ и неотрицательно определена, то есть $\forall g: X \rightarrow \mathbb{R}, \int_X \int_X K(x, x')g(x)g(x')dxdx' \geqslant 0$ |
Таким образом мы видим, что класс ядер достаточно широк.
Проверка неотрицательной определённости функции в реальных задачах может быть сложной. Чаще всего ограничиваются перебором конечного числа функций, про которые известно, что они являются ядрами. Среди них выбирается лучшая (обычно по критерию скользящего контроля). Такое решение не будет оптимальным, и на сегодняшний день проблема выбора ядра, оптимального для данной конкретной задачи, остаётся открытой, лучшие из известных на данный момент решений основываются на генетических алгоритмах[1].
Конструктивные способы построения ядер
1. Произвольное скалярное произведение $ K(x,x') =\langle x,x'\rangle $ является ядром.
2. Константа $K(x,x') = 1$ является ядром.
3. Произведение ядер $K(x,x')=K_1(x,x')K_2(x,x')$является ядром.
4. Для любой функции $\psi :X\rightarrow R$ произведение $K(x,x′) =\psi(x)\psi(x')$— ядро.
5. Линейная комбинация ядер с неотрицательными коэффициентами $K(x,x')=\alpha_1K_1(x,x') +\alpha_2K_2(x,x')$является ядром.
6. Композиция произвольной функции $\varphi:X \rightarrow X$ и произвольного ядра $K_0$ является ядром: $K(x,x')=K_0(\varphi(x),\varphi(x'))$.
7. Если $s:X×X\rightarrow R$ произвольная симметричная интегрируемая функция, то $K(x,x′) =\int_Xs(x,z)s(x',z)dz$ является ядром.
8. Функция вида $K(x,x') = k(x−x')$ является ядром тогда и только тогда, когда Фурье-образ $F[k](\omega) = (2\pi)^{\frac{n}{2}}\int_Xe^{−i\langle\omega,x\rangle }k(x)dx$ неотрицателен.
9. Предел локально-равномерно сходящейся последовательности ядер — ядро.
10. Композиция произвольного ядра $K_0$ и произвольной функции $f:R\rightarrow R$, представимой в виде сходящегося степенного ряда с неотрицательными коэффициентами $K(x,x') = f(K_0(x,x'))$, является ядром. В частности, функции $f(z) =e^z$ и $f(z) =\frac{1}{1−z}$ где $z$ — функция ядра — являются ядрами.
Некоторые часто используемые ядра
0. Линейное (англ. linear) $K(x, x')= \langle x, x'\rangle$
Используется в алгоритме SVM по умолчанию.
1. Полиномиальное (англ. polynomial) $K(x, x') = (\langle x, x' \rangle + R)^d$[2]
Используется когда необходимо получить полином $p(y)$, где в качестве $y$ выступает скалярное произведение $\langle x, x' \rangle$. Поскольку в конструктивных возможностях у нас есть умножение ядер, умножение на коэффициент и сложение, то любой многочлен так же является ядром.
2. Гаусово (англ. gaussian) ядро RBF (Radial basis function)[3] $K(x, x') = exp(-\frac{\parallel x - x'\parallel^2}{2\sigma^2})$
Такое ядро соответствует бесконечномерному пространству. Поскольку оно является пределом последовательности полиномиальных ядер при стремлении степени ядра к бесконечности.
3. Сигмоидальное (англ. sigmoid) ядро $tangh (\gamma \langle x, x'\rangle + r)$
В отличие от предыдущих 3-х не является ядром Мерсера (не выполняет условие теоремы), но при этом на практике работает хорошо.
4. Строковое
Строковые ядра [4] это различные ядерные функции для вычисления расстояний между двумя строками.
Использование ядер в коде
В библиотеке языка Python — sklearn.clustering[5], есть функции и классы которые используют ядра для кластеризации.
- Подключаем библиотеки:
import numpy as np from sklearn.datasets import make_blobs from sklearn.cluster import mean_shiftU
- Генерируем данные:
centers = [[1, 1], [-1, -1], [1, -1]] X, _ = make_blobs(n_samples=10000, centers=centers, cluster_std=0.6)
- Посчтитаем кластеризацию с помощью MeanShift[6], находим разделяющуу полосу, добавляя в качестве первого парамента значение для пропускной способности ядра:
bandwidth = estimate_bandwidth(X, quantile=0.2, n_samples=500)
ms = MeanShift(bandwidth=bandwidth, bin_seeding=True)
ms.fit(X)
labels = ms.labels_
cluster_centers = ms.cluster_centers_
labels_unique = np.unique(labels)
n_clusters_ = len(labels_unique)
print("number of estimated clusters : %d" % n_clusters_)
См. также
Примечания
- ↑ - T.Howley, M.G.Madden — An Evolutionary Approach to Automatic Kernel Construction
- ↑ https://en.wikipedia.org/wiki/Polynomial_kernel - Polynomial kernel
- ↑ - RBF
- ↑ - Строковое ядро
- ↑ https://scikit-learn.org/stable/modules/classes.html#module-sklearn.cluster - sklearn.cluster
- ↑ https://scikit-learn.org/stable/modules/generated/sklearn.cluster.MeanShift.html#sklearn.cluster.MeanShift - Meanshift documentaion