Граф блоков-точек сочленения

Определение:

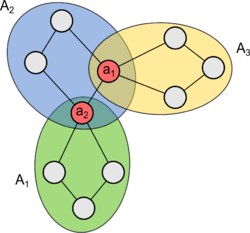
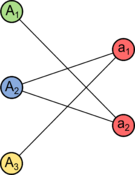
Пусть граф [math]G[/math] связен. Обозначим [math]A_1...A_n[/math] — блоки, а [math]a_1...a_m[/math] — точки сочленения [math]G[/math]. Построим двудольный граф [math]T[/math], поместив [math]A_1...A_n[/math] и [math]a_1...a_m[/math] в различные его доли. Если точка сочленения принадлежит блоку, проведем между ними ребро. Полученный граф [math]T[/math] называют графом блоков-точек сочленения (англ. block cutpoint graph) графа [math]G[/math].

Граф [math]G[/math]

Граф [math]T[/math]

Лемма:

В определении, приведенном выше, [math]T[/math] — дерево.

См. также

• Граф компонент реберной двусвязности

Источники информации

• Асанов М. О., Баранский В. А., Расин В. В. Дискретная математика: графы, матроиды, алгоритмы — НИЦ РХД, 2001. — 288 с. — ISBN 5-93972-076-5