Вписывание части изображения

Материал из Викиконспекты
Версия от 01:28, 11 января 2021; Fedleonid (обсуждение | вклад) (→‎Deep Image PriorDeep Image Prior, Dmitry Ulyanov, Andrea Vedaldi, Victor Lempitsky)
Перейти к: навигация, поиск
Эта статья находится в разработке!
Рисунок 1. Пример восстановления изображения. (a) — оригинальное изображение, (b) — изображение со стертыми частями, (с) — изображение, полученное в результате восстановления.[1]

Восстановление изображения (англ. inpainting) — это процесс замены поврежденных частей изображения на реалистичные фрагменты. Вписывание части изображения — это подзадача восстановления, которая опирается на имеющуюся неиспорченную часть изображении для замены поврежденной.

Методы данной области применяются для редактирования изображений или для их восстановления, если их часть была утрачена или повреждена. С помощью современных моделей можно вырезать ненужные объекты или изменить их внешний вид (например, поменять цвет глаз у человека).


Виды восстановления изображения

Рисунок 2. Пример устранения наложенного текста на изобрежение. В данном случае текстом покрыто 18.77% площади.[2]

Восстановление изображения разделяется на две задачи:

  • Управляемое восстановление изображения (англ. non-blind inpainting). В этой задаче вместе с изображением подается информация о том, какие пиксели нужно заменить.
  • Слепое восстановление изображения (англ. blind inpainting). В решениях данной проблемы модель сама определяет, где на изображении поврежденные пиксели. Модели слепого восстановления чаще всего занимаются устранением шумов (англ. denoising). В качестве шума, например, может быть наложенный текст (см Рис. 2).

В этом конспекте преимущественно речь пойдет про управляемое восстановление.

Традиционные методы

Для решения данной задачи существует множество различных методов, в том числе простых. Почти все простые методы основаны на следующей концепции: заполнение отсутствующих частей пикселями, идентичными соседним пикселям или похожими на них. Такие методы наиболее подходят для задачи устранения шума или небольших дефектов изображения. Но на изображениях, где отсутствует значительная часть данных, эти методы дают плохое качество изображения на выходе.

Есть два основных простых метода восстановления данных:

  1. Быстрый пошаговый метод (англ. Fast marching method)[3]. Этот метод двигается от границ области, которую нужно заполнить, к ее центру, постепенно восстанавливая пиксели. Каждый новый пиксель вычисляется как взвешенная сумма известных соседних пикселей.
  2. Метод Навье-Стокса (англ. Navier-Stokes method)[4]. Метод основывается на том, что границы объектов на изображении должны быть непрерывными. Значения пикселей вычисляются из областей вокруг испорченной части. Метод основывается на дифференциальных уравнениях в частных производных.

Глубокое обучение

Рисунок 3. Пример GAN для inpainting.[5]

В отличие от приведенных выше методов, глубокое обучение позволяет в процессе восстановления изображения учитывать его семантику. В этом случае алгоритм заполнения отсутствующих областей основывается на том, какие объекты расположены на изображении.

Для того, чтобы понимать, какую часть изображения нужно заполнить, на вход сети кроме самого изображения подается слой маски с информацией об испорченных пикселях.

Сети обычно имеют модель автокодировщиков (autoencoder) — сначала идут слои кодирующие, а потом декодирующие изображение. Функция потерь заставляет модель изучать другие свойства изображения, а не просто копировать его из входных данных в выходные. Именно это позволяет научить модель заполнять недостающие пиксели.

Обучение может происходить через сравнение оригинального изображения и синтетического, сгенерированного сетью или через генеративно-состязательную сеть (GAN). Во втором случае для обучения используется дискриминатор, который определяет настоящее ли изображение подали ему на вход. В современных моделях обычно используют совмещенный подход: функции потерь зависят и от исходного изображения, и от выхода дискриминатора.

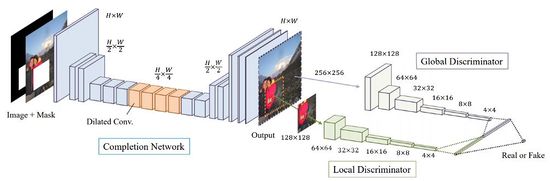
В ранних моделях часто применялись два дискриминатора (см Рис. 3):

  1. Локальный дискриминатор (англ. Local Discriminator). Ему подавалась на вход только сгенерированная часть изображения.
  2. Глобальный дискриминатор (англ. Global Discriminator). В данном случае на вход подавалось все изображение целиком.

Однако в современных моделях используется один дискриминатор, который принимает на вход не только восстановленное изображение, но и маску. Современные модели чаще всего принимают на вход маски произвольной формы (англ. free-form mask), при работе с которыми локальный дискриминатор показывает плохое качество. Именно поэтому концепция двух дискриминаторов стала непопулярной.

Свертки

Для вписывания изображения помимо классической свертки широко используются другие способы перехода от слоя к слою. Подробнее про свертки можно прочитать в конспекте Сверточные нейронные сети

  1. Расширенная свертка (англ. Dilated convolution). Данный способ позволяет сохранить качество изображении, уменьшив затраты на память и вычисления.
  2. Частичная свертка (англ. Partial convolution). Данная свертка дает лучшее качество на масках произвольной формы. Классическая свертка предполагает, что все пиксели валидны, а частичная учитывает количество стертых пикселей в рассматриваемой матрице.
  3. Стробированная свертка (англ. Gated convolution). Данная свертка позволяет сохранять информацию о маске и эскизах пользователя во всех слоях сети, что дает возможность получить лучшее качество.

Функции потерь

Существует большое множество различных функций потерь при методе обучения модели через сравнение сгенерированного изображения с оригинальным. Примеры:

  • L1-loss или Per-pixel loss. Оценивает точность восстановления каждого пикселя по отдельности.


[math]L_{per-pixel} = \frac{1}{N_{I_{gt}}}\|M \odot (I_{gen} - I_{gt})\| + \alpha \frac{1}{N_{I_{gt}}}\|(1 - M) \odot (I_{gen} - I_{gt})\|[/math]
[math]I_{gen}[/math] — выход генератора; [math]I_{gt}[/math] — оригинальное изображние (англ. ground truth); [math]N_a[/math] — количество элементов в объекте [math]a[/math]; [math]M[/math] — бинарная маска; [math]\alpha[/math] — гиперпараметр, [math]\odot[/math] — поэлементное перемножение.
  • Perceptual loss. Cравнивает признаки сгенерированного и исходного изображений, полученные с помощью модели VGG-16[6].


[math]L_{percept} = \sum\limits_{q}\frac{\|\Theta_{q}(I_{gen}) - \Theta_{q}(I_{gt})\|}{N_{\Theta_{q}(I_{gt})}} + \sum\limits_{q}\frac{\|\Theta_{q}(I_{comp}) - \Theta_{q}(I_{gt})\|}{N_{\Theta_{q}(I_{gt})}}[/math]
[math]I_{comp}[/math] — изображение [math]I_{gen}[/math], в котором нестертые части заменены на части из [math]I_{gt}[/math]; [math]\Theta_{q}(x)[/math] — карта признаков, полученная [math]q[/math]-ым слоем VGG-16.
  • Style loss. Сравнивает текстуру и цвета изображений, используя матрицу Грама[7].


[math]L_{style} = \sum\limits_{q}\frac{1}{C_q C_q} \| \frac{G_q(I_{gen})-G_q(I_{gt})}{N_q}\|[/math]
[math]G_q(x) = (\Theta_{q}(I_{x}))^T (\Theta_{q}(I_{x}))[/math] — матрица Грама для выполнения автокорреляции на карте признаков VGG-16; [math]C_{q}[/math] — размерность матрицы Грама.
  • Total variation loss. Оценивает однородность полученного изображения.


[math]L_{tv} = \sum\limits_{(i,j) \in R}\frac{I_{comp}^{i,j+1} - I_{comp}^{i,j}}{N_{I_{comp}}} + \sum\limits_{(i,j) \in R}\frac{I_{comp}^{i+1,j} - I_{comp}^{i,j}}{N_{I_{comp}}}[/math]
  • Adversarial loss. Сравнивает генерируемые и оригинальные границы объектов в изображении.


[math]L_{adv} = \mathbb{E}[\log D(H_{gt}, I_{gray})] + \mathbb{E}[\log (1 - D(H_{gen}, I_{gray}))][/math]
[math]I_{gray}[/math] — черно-белое оригинальное изображение; [math]H_{gt}[/math] — границы объектов оригинального изображения; [math]H_{gen}[/math] — генерируемые границы; [math]D[/math] — дискриминатор;
  • Feature-matching loss. Сравнивает изображения по признакам, извлекаемыми из всех слоев дискриминатора.


[math]L_{FM} = \mathbb{E}[\sum\limits_{i=1}^L \frac{1}{N_i} \|D^{(i)}(H_{gt} - D^{(i)}(H_{gen}))\| ][/math]
[math]L[/math] — количество слоев дискриминатора; [math]N_i[/math] — число нейронов на [math]i[/math]-ом слое дискриминатора; [math]D^{(i)}[/math] — значения диксриминатора на слое [math]i[/math];

При обучении обычно используется комбинация функций потерь с некоторыми весами, которые являются гиперпараметрами. В моделях, где вдобавок используется дискриминатор, функция потерь от его выхода также подмешивается к итоговой функции потерь.

Примеры современных моделей

Рисунок 4. Пример работы модели SC-FEGAN.[1]

SC-FEGAN[1]

SC-FEGAN позволяет производить высококачественные изображения лиц за счет эскизов, передаваемых пользователем вместо стертых частей изображения. Иными словами пользователь может стереть фрагмент, который он хочет изменить, нарисовать на его месте желаемый объект, и полученный эскиз, а также его цветовая палитра, будут отражены в сгенерированном фрагменте.

Дискриминатор данной сети принимает на вход сгенерированное изображение, маску и рисунок пользователя. Итоговая функция потерь формируется из выхода дискриминатора и функций сравнения изображения с оригинальным (per-pixel loss, perceptual loss, style loss).

Рисунок 5. Сеть DeepFillv2.[8]

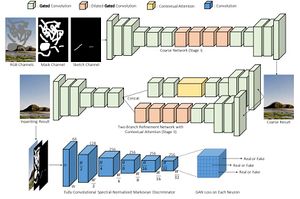
DeepFillv2[8]

Главная идея этой модели — использование стробированной свертки, которая позволила добиться хорошего качества вписывания при восстановлении изображения с разными формами испорченных областей. Также можно использовать рисунок пользователя в качестве входных данных.

В данной модели используется вариант генеративно-состязательной сети — SN-PatchGAN. Дискриминатор этой сети в каждой точке вычисляет кусочно-линейную функцию потерь, формируя таким образом [math]h \times w \times c[/math] генеративно-состязательных сетей, каждая из которых сосредотачивается на различных частях и свойствах изображения. Генератор, состоящий из двух сетей (грубой и сети повышающей качество изображения), используют модель кодировщик-декодировщик вместо U-Net[9], в которой все слои классической свертки заменены на стробированные.

Pluralistic Image Completion[10]

Главное отличие этой модели от других — способность выдавать несколько вариантов заполнения отсутствующих областей изображения. Обычно модели генерируют только один вариант, пытаясь приблизиться к оригинальному изображению. Используя же данную модель, человек может выбрать то сгенерированное изображение, которое выглядит более реалистичным, получая таким образом более качественные изображения на выходе.

Данная модель добивается такого эффекта путем пропускания входного изображения через две параллельные сети. Первая сеть — реконструирующая. Она пытается приблизить выходное изображение к оригинальному. Вторая сеть — генерирующая, работающая с априорным распределением отсутствующих областей и выборками известных пикселей. Каждая сеть имеет свой дискриминатор, помогающий обучить модель. Кроме выхода дискриминатора для обучения также используются функции сравнения полученного изображения с оригинальным.

Рисунок 6. Пример работы модели EdgeConnect.[11]

EdgeConnect[11]

EdgeConnect разбивает задачу вписывания на две части:

  1. Выделение границ изображения и предсказание границ утраченной части изображения.
  2. Использование сгенерированных границ для заполнения утраченной части изображения.

В обоих частях используется генеративно-состязательная сеть. Генераторы состоят из кодировщика, нескольких остаточных блоков с расширенной сверткой и декодировщика. Для дискриминатора используется PatchGAN[12].

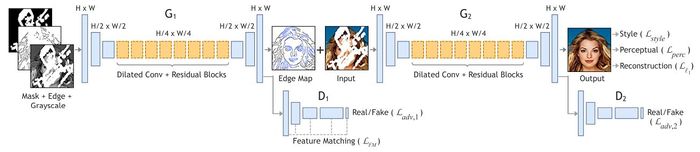Рисунок 7. Сеть EdgeConnect. [math]G_1[/math] — генератор границ, [math]G_2[/math] — генератор изображения, [math]D_1[/math] и [math]D_2[/math] — дискриминаторы.[11]

Для генерации ребер сначала выделяются границы существующей части изображения с помощью Canny edge detector[13]. Потом полученная граница вместе с маской и черно-белым изображением дается генератору. В качестве целевой функции потерь для тренировки сети берется комбинация двух функций: adversarial loss и feature-matching loss. Также для стабилизация обучения генератора и дискриминатора используется спектральная нормализация.

Для восстановления генератор получает на вход испорченное изображение и границы, которые составлены из реальных и сгенерированных на предыдущем этапе. В результате генерируется полное изображение. Так же, как и на предыдущем этапе, используется составная функция потерь из adversarial loss, perceptual loss и style loss.

Однако сети не удается предсказать достаточно хорошую границу, если отсутствует большая часть изображения или объект имеет сложную структуру.

Также данную модель можно использовать для соединения двух изображений или удаления лишних объектов с фотографий.

Рисунок 8. Пример соединения двух изображения моделью EdgeConnect.[11]

Deep Image Prior[14]

Рисунок 9. Процесс восстановления изображения с помощью Deep Image Prior.[14]

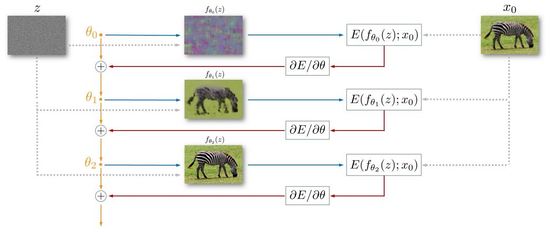
Как известно, большинство методов глубокого обучения требуют больших наборов данных для тренировки. В отличие от них Deep Image Prior не требует никакой предварительной обучающей выборки кроме одного изображения, которое надо исправить. Для этого сеть учится извлекать полезную информации из самого обрабатываемого изображения. Данный метод применяется для таких задач как вписывание части изображения, удаление шума и увеличение разрешения фотографий.

Сформулируем данную задачу как задачу минимизации:

[math]\theta^{*} = \underset{\theta} {\mathrm{argmin}} ~E(f_{\theta}(z), x_0), \;\; x^{*} = f_{\theta^{*}}(z) \;\; (1)[/math]

[math]E(x, x_0)[/math] — это функция потерь, зависящая от решаемой задачи, а [math]f_{\theta}(z)[/math] — некоторая сверточная сеть.

Алгоритм решения задачи (см Рис. 9):

  1. Инициализируем [math]\theta[/math] случайными весами.
  2. На каждой итерации:
    1. Сеть [math]f[/math] с текущими весами [math]\theta[/math] получает на вход фиксированный тензор [math]z[/math] и возвращает восстановленное изображение [math]x[/math].
    2. С помощью сгенерированного изображения x и исходного изображения [math]x_0[/math] вычисляется функция потерь [math]E(x;x0)[/math].
    3. Веса [math]\theta[/math] обновляются так, чтобы минимизировать уравнение (1).

В качестве [math]f[/math] предлагается использовать сеть U-net с пропускающими соединениями.

Для вписывания части изображения используется следующая функция потерь: [math]E(x, x_0) = \|(x - x_0) * m \|^2[/math], где [math]m[/math] — маска.

См. также

Примечания

  1. ↑ 1,0 1,1 1,2 Face Editing Generative Adversarial Network with User's Sketch and Color, Youngjoo Jo, Jongyoul Park
  2. ↑ Fast Digital Image Inpainting, Manuel M. Oliveira, Brian Bowen, Richard McKenna, Yu-Sung Chang
  3. ↑ An Image Inpainting Technique Based onthe Fast Marching Method, Alexandru Telea
  4. ↑ Navier-Stokes, Fluid Dynamics, and Image and Video Inpainting, M. Bertalmio, A. L. Bertozzi, G. Sapiro
  5. ↑ Globally and Locally Consistent Image Completion, Satoshi Lizuka, Edgar Simo-Serra, Hiroshi Ishikawa
  6. ↑ Very Deep Convolutional Networks for Large-Scale Image Recognition, Karen Simonyan, Andrew Zisserman
  7. ↑ Gramian matrix, Wikipedia
  8. ↑ 8,0 8,1 Free-Form Image Inpainting with Gated Convolution, Jiahui Yu, Zhe Lin, Jimei Yang, Xiaohui Shen, Xin Lu, Thomas Huang
  9. ↑ U-Net: Convolutional Networks for Biomedical Image Segmentation, Olaf Ronneberger, Philipp Fischer, Thomas Brox
  10. ↑ Pluralistic Image Completion, Chuanxia Zheng, Tat-Jen Cham, Jianfei Cai
  11. ↑ 11,0 11,1 11,2 11,3 EdgeConnect: Generative Image Inpainting with Adversarial Edge Learning, Kamyar Nazeri, Eric Ng, Tony Joseph, Faisal Z. Qureshi, Mehran Ebrahimi
  12. ↑ PatchGan, PapersWithCode
  13. ↑ Canny edge detector, Wikipedia
  14. ↑ 14,0 14,1 Deep Image Prior, Dmitry Ulyanov, Andrea Vedaldi, Victor Lempitsky

Источники информации

Источник — «http://neerc.ifmo.ru/wiki/index.php?title=Вписывание_части_изображения&oldid=77393»