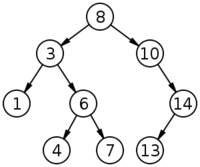
Дерево поиска, наивная реализация

Бинарное дерево поиска из 9 элементов

Бинарное дерево поиска (англ. binary search tree, BST) - структура данных для работы с динамическими множествами.

Бинарное дерево поиска должно обладать следующим свойством: Если x - узел бинарного дерева с ключом k, то все узлы в левом поддереве должны иметь ключи, меньшие k, а в правом поддереве большие k.

Операции в бинарном дереве поиска

обход дерева поиска

Имеется простой алгоритм вывода всех ключей бинарного дерева поиска в отсортированном порядке.

Tree_walk(node x)
   if(x != null)
      Tree_walk(x.left);
      print(x.key);
      Tree_walt(x.right);

Данный алгоритм выполняет обход за время [math]O(n)[/math], поскольку процедура вызывается ровно два раза для каждого узла дерева. Корректность данного алгоритма следует из свойств бинарного дерева поиска.

поиск элемента

Для поиска элемента в бинарном дереве поиска можно воспользоваться следующей процедурой.

Tree_search(node x, key k)
   if x == null or k == x.key
      return x
   if k < x.key
      return Tree_search(x.left, k)
   else
      return Tree_search(x.right, k)

Приведенная выше функция принимает в качестве параметров корень дерева и искомый ключ. Для каждого узла функция сравнивает значение его ключа с искомым ключом. Если ключи одинаковы, то функция возвращает текущий узел, в противном случае функция вызывается рекурсивно для левого или правого поддерева. Узлы, которые посещает функция образуют нисходящий путь от корня, так что время ее работы [math]O(h)[/math], где [math]h[/math] - высота дерева.

поиск минимума и максимума

Чтобы найти минимальный элемент в бинарном дереве поиска, необходимо просто следовать указателям left от корня дерева, пока не встретится значение hull. Если у вершины есть левое поддерево, то по свойству бинарного дерева поиска в нем хранятся все элементы с меньшим ключом. Если его нет, значит эта вершина и есть минимальная. Аналогично ищется и максимальный элемент. Для этого нужно следовать правым указателям.

Tree_min(root x)
  while (x.left != null)
     x = x.left
  return x

Tree_max(root x)
  while (x.right != null)
     x = x.right
  return x

Данные функции принимают корень дерева, и возвращают минимальный(максимальный) элемент в дереве. Обе процедуры выполняются за время [math]O(h)[/math].

поиск следующего и предыдущего элемента

Tree_next(root x)
   if (x.right != null)
      return Tree_min(x.right)
   else
      

Если у узла, следующий элемент которого мы хотим найти, есть правое поддерево, то следующий за ним элемент - минимальный в этом поддереве. Иначе нужно следовать вверх, пока не будет найден узел, являющийся левым потомком своего родителя.

вставка

Операция вставки работает аналогично поиску элемента, только при обнаружении нулевого указателя нужно подвесить на него вставляемый элемент. Приведем итеративную реализацию этого алгоритма.

Литература

1. Кормен, Т., Лейзерсон, Ч., Ривест, Р., Штайн, К. Алгоритмы: построение и анализ = Introduction to Algorithms / Под ред. И. В. Красикова. — 2-е изд. — М.: Вильямс, 2005. — 1296 с. — ISBN 5-8459-0857-4