Задача планирования движения

Материал из Викиконспекты
Версия от 20:10, 21 января 2021; NikolayPlyusnin (обсуждение | вклад) (→‎Решение проблемы для беспилотных автомобилей (self-driving cars))
Перейти к: навигация, поиск
Эта статья находится в разработке!

Планирование движения, а также планирование пути (также известное как проблема навигации) — это вычислительная проблема для поиска последовательности допустимых конфигураций, которая перемещает объект от источника к месту назначения.

Постановка задачи

Задача:
Пусть задана сцена как непустое множество препятствий [math]O \subset W[/math] в области евклидова пространства [math]W \subset E^N,\ N \in \{2,3\}[/math]. Пусть также задано твердое тело либо кинематическая цепь [math]A \subset W[/math] либо кинематическая цепь [math]A \langle B, J \rangle[/math], где [math]B = \{B_1, B_2, \dots, B_n\} \subset W[/math] — множество твердотельных звеньев, а [math]J = (J_1, J_2, \dots, J_k)[/math] — множество кинематических ограничений таких, что при корректной конфигурации цепи предикаты ограничений [math]J_1(c), J_2(c), \dots, J_k(c)[/math] принимают истинное значение. Под конфигурацией [math]c \in C_A[/math] здесь понимается набор значений параметров, однозначно определяющий положение точек объекта [math]A[/math] в пространстве сцены. Обычно используется минимальный набор параметров, соответствующий количеству степеней свободы объекта и определяющий пространство состояний или конфигурационное пространство объекта [math]C_A[/math].


Определение:
Пространством допустимых состояний назовем множество всех конфигураций объекта [math]c \in C_A[/math], удовлетворяющих кинематическим ограничениям и исключающих столкновения с препятствиями сцены [math]C_{free} = \{c \in C_A | J_1(c) \wedge J_2(c), \dots, \wedge J_K(c) \wedge B_1(c) \cap O = \varnothing,…, B_n(c) \cap O = \varnothing\}[/math]. Для простого твердого тела свободное множество определяется как [math]C_{free} = \{c \in C_A | A(c) \cap O = \varnothing\}[/math]. Тогда постановка задачи поиска пути может быть сформулирована следующим образом. 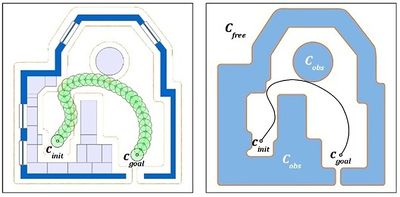Для пары заданных бесконфликтных конфигураций [math]c_{init},\ c_{goal} \in C_{free}[/math] требуется найти непрерывный путь [math]p(\tau): [0,1] \rightarrow C_{free}[/math] такой, что [math]p(0) = c_{init}[/math] и [math]p(1) = c_{goal}[/math]


Рис. 1. Конфигурационные пространства двумерного твердого тела[1]
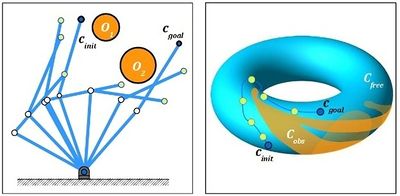Рис. 2. Конфигурационные пространства двухзвенного манипуляционного робота[1]

Поскольку планирование маршрута, как правило, допускает бесконечное множество решений (хотя может не существовать ни одного решения), иногда данную задачу формулируют в постановке оптимизационной задачи с целевой функцией, соответствующей минимальной длине маршрута или максимальной удаленности перемещаемого объекта от препятствий. На практике поиск пути даже в простых сценах с относительно небольшим количеством препятствий становится трудноразрешимой задачей, если перемещаемый объект имеет сложную геометрию или высокое число степеней свободы. В современных индустриальных приложениях часто требуется моделировать поведение сложных кинематических систем с шестью и более степенями свободы статическом или динамическом окружении,насчитывающим тысячи препятствий.

Этапы

Восприятие/анализ обстановки

Анализ данных об окружении, выделение объектов и препятствий, определение их размеров, скоростей, и расстояний до них. Зачастую осуществляется путем применения алгоритмов машинного обучения для распознавания объектов на изображениях и прочих массивах данных (таких как данные с датчиков).

Предсказание движения объектов

Анализ собранных за время наблюдения данных об окружающих объектов для последующего построение модели их движения и предсказания их траекторий. См. Предсказание траекторий движения объектов

Принятие решения/планирование траектории движения

Построение потенциальных траекторий движения и выбор итоговой на основе собранных на предыдущих этапах данных. Как правило осуществляется с помощью дискретизации пространства и последующего применения алгоритмов на графах (таких как A*, RRT*, и прочих вариаций RRT, а также других, см. далее) для поиска оптимальной траектории. В последнее время также становятся более актуальными решения с применением машинного обучения --- в частности, подходы на основе имитационного обучения и обратного обучения с подкреплением, обученные на большом количестве примеров, предоставленных человеком[2].

Предсказание траекторий движения объектов

Поскольку в общем случае мы не можем однозначно знать, как будут двигаться объекты, для предсказания траекторий их движений необходимо строить модели на основе прошлых измерений. Эти модели могут представлять из себя как простые предсказания (например, “объект продолжит двигаться с неизменной скоростью/ускорением”), так и более сложные алгоритмы.

Стандартный подход

Одна из основных сложностей в предсказании траекторий движения объектов заключается в неопределенности, которая появляется из-за погрешностей в измерениях сенсоров и невозможности однозначно предсказать действия объектов. Для смягчения этой проблемы применяются фильтры, которые приближают текущую позицию исходя из измерений сенсоров и наших предсказаний, а также степени уверенности в результатах обоих.

Также проблематичным является тот факт, что одной модели (особенно простой) как правило недостаточно для описания траектории движения объекта. В связи с этим существует алгоритм множества взаимодействующих моделей (Interacting Multiple Model, IMM) — подход применения сразу нескольких моделей, для каждой из которых поддерживается актуальная (меняющаяся по мере прошествия времени и получения новых измерений) вероятность того, что объект двигается согласно этой модели. Таким образом, используя, например, по модели для каждого возможного движения (поворот, ускорение, и так далее), мы можем делать более точные предположения о том, где объект будет находиться в будущем.

Существуют и другие, более специализированные, подходы, опирающиеся на ряд заранее заданных правил, моделей и предположений об используемом пространстве.

Применение машинного обучения

Стандартные инженерные подходы (в том числе IMM) также обладают своими недостатками как в точности (особенно при необходимости долговременного предсказания), так и в скорости, в связи с чем появились и подходы, использующие машинное обучение, в частности — рекуррентные нейронные сети.

Они применяются как для улучшения производительности самого алгоритма IMM (например, для улучшения точности в пересчете вероятностей[3]), так и для его замены (иногда применяя тот же самый принцип[4]).

Существуют и другие алгоритмы, основанные на машинном обучении (в основном использующие сверточные нейронные сети), и не опирающиеся на принцип работы IMM, вместо этого по большей части использующие большие массивы сгенерированных человеком данных[5][6][7].

Решение проблемы для беспилотных автомобилей (self-driving cars)

Для организации управления беспилотным автомобилем можно воспользоваться классическим подходом из робототехники. Задача самостоятельного передвижения разбивается на четыре модуля.

  • Модуль локализации отвечает за определение положения автомобиля в пространстве.
  • Модуль распознавания — за анализ окружающей обстановки.
  • Модуль планирования — за планирование маршрута исходя из обстановки и цели.
  • Модуль управления — за определение траектории движения в выбранном направлении.

Тем не менее такая модель все еще имеет множество проблем, которые необходимо решить. Автомобиль обладает рядом довольно существенных ограничений. У автомобиля есть текущее направление, угол поворота колес, и он не может просто оказаться на два метра левее от текущего местоположения, это очень сложно. Он может ехать примерно вперед, поворачивая на какой-то угол, но тем не менее, перемещение очень сильно ограничено. И на траекторию движения влияют ограничениям, которые следуют из кинематики. Например, невозможно мгновенно разогнаться и мгновенно увеличить свое ускорение.

Для планирования дальнейшего движения автомобиля можно использовать нейросети, передавая информацию со всех датчиков и камер в нейросеть, предварительно ее обучив на человеческих перемещениях. Обучить, в каких ситуациях куда нужно крутить руль, увеличивать или снижать скорость и т.д. В теории такой подход представляется хорошим решением проблемы, но на практике выяснилось, что нужно все-таки слишком много данных, нужна слишком большая нейросеть, чтобы за человеком все успешно повторять в различных ситуациях. В этом направлении ведется активная работа, и пока большинство успешных решений проблемы опирается на нейросети лишь частично, доверяя бо́льшую часть работы проверенным алгоритмам.

Алгоритмы на графах

Существует несколько алгоритмов на графах, позволяющих решить проблему, но для их использования нужно понять, как построить граф по имеющейся информации. Для этого аналогично существует несколько подходов:

  • Разбиение пространства на клетки и построение графа на них.
  • Построение графа из регулярных примитивов движения (например, дуг).
  • И другие, более специализированные подходы, основанные на особенностях конкретной системы.

Самым популярным и зачастую самым оптимальным является алгоритм А*.

Преимущества:

  • Гарантированно находит кратчайший (в дискретизированном пространстве) путь.

Недостатки:

  • В пространствах малой размерности путь редко является кинематически выполнимым (зависит от метода построения графа).
  • В пространствах большой размерности время работы заметно ухудшается.

Оптимизационные алгоритмы

Идея этого вида алгоритмов заключается в следующем: рассмотрим траекторию нашего положения во времени, [math]x[/math] и [math]y[/math], зависящие от времени [math]t[/math], то есть поймем, в какой точке мы хотим оказаться в момент времени [math]t[/math]. Не составит труда определить угол касательной через арктангенс от производных, можно сказать, что оптимальной в этом случае будет траектория, которая минимизирует функционал, являющийся интегралом по времени вперед от какой-то функции от траектории. Функция от траектории здесь каким-либо образом нас штрафует за резкие повороты, резкие разгоны, нахождение близко к препятствиям и т. д. Тогда, если просуммировать вдоль траектории все необходимые штрафы и попытаться это минимизировать стандартным математическим аппаратом, никак не связанным с автомобилями в целом и беспилотными автомобилями в частности, то это решит задачу в каком-то общем виде.

Что лучше рассмотреть в качестве штрафов? Например, можно сказать, что не нужно подъезжать близко к препятствиям, учитывать это с каким-то весом, или что скорость не должна быть гораздо выше или ниже заранее определенной скорости. Можно штрафовать за вторую производную, которая является ускорением, потому что машина не должна резко ускоряться или замедляться.

Можно рассмотреть третью производную, которая является рывком, то есть не нужно, чтобы ускорение тоже менялось достаточно резко, поскольку это может сказаться на состоянии пассажиров. Если ускорение фиксированное и машина просто все время разгоняется, то, как показывают исследования, людей не укачивает. Также можно избегать крутых поворотов, ограничивая угол. Есть дополнительные ограничения, которые говорят, что машина физически не может разгоняться быстрее какого-то ускорения. Если все это учтется, то можно решить задачу с помощью абстрактного алгоритма минимизации функции и получить некий результат.

Большинство методов оптимизации предпочитают работать с хорошо дифференцируемыми функциями, в то время как автомобиль — объект довольно сложной формы, и препятствия, которые он объезжает, это тоже объекты непростых форм. Поэтому нужно производить какие-то упрощения. Например, можно сказать, что машина — не что-то сложное, а просто пять окружностей.

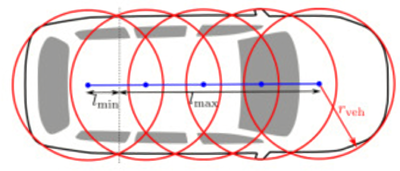Рис. 3. Для удобства вычисления расстояний представим автомобиль в виде набора окружностей[8]
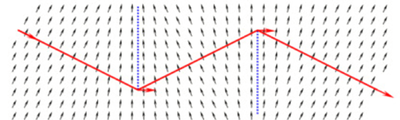Рис. 4. Для плавной функции расстояния до препятствий введем поле градиентов[8]

От окружностей очень легко считать расстояния до чего угодно и очень легко проверять окружность на пересечения с остальными геометрическими примитивами. Если расстояние до центра меньше, чем радиус, то вот пересечение, иначе все хорошо.

Что нужно, чтобы плавно изменялось расстояние? Евклидово расстояние до невыпуклых многоугольников не обладает необходимыми нам свойствами и плохо дифференцируемо в местах, где возникает отсутствие выпуклости. Поэтому мы можем построить такое псевдо расстояние по градиентному полю до нашей ломаной, она здесь обозначена красным и представляет собой препятствие. Мы можем довольно несложно ввести поле расстояний от каждой точки до этой ломаной, которая направлена в сторону ломаной и обладает необходимыми свойствами дифференцируемости — пусть и не являясь строго кратчайшей. Если мы все это сделаем — сможем построить гладкую, красивую и аккуратную траекторию.

Преимущества:

  • Пространство управления непрерывно.

Недостатки:

  • Сходится к локальным минимумам.
  • Ограничения должны быть заданы дифференцируемыми функциями.

К преимуществам таких методов мы относим то, что получается хорошая траектория и пространство управления непрерывно. Мы можем по нему ехать, все ограничения в той или иной степени соблюдаются. Но к сожалению, большинство оптимизационных методов или даже почти все так или иначе страдают от локальных минимумов, где их попытки что-либо оптимизировать застревают и не находят достаточно хорошего решения. Очень сложно все формулировать в виде математических дифференцируемых функций, это тоже не всегда получается.

Однако выход есть. Мы можем применить алгоритмы, которые работают некоторым случайным образом, но зато позволяют нам построить какой-то приближенный маршрут достаточно быстро и удобно. Например, мы будем строить наш граф, являющийся деревом, итеративным образом. Вначале ничего делить на клеточки не будем, никаких примитивов строить не будем. Мы просто возьмем симулятор нашей машины, который в целом умеет симулировать движение, максимально похожее на то, как машина едет по-настоящему. И возьмем стартовую точку. После этого итеративно выберем случайную точку в пространстве. И — найдем в текущем построенном дереве ближайший к ней узел. Построим ребро в сторону этой точки с помощью симуляции проезда в эту сторону.

Получается, мы каждый раз едем от нашего построенного дерева в случайную сторону и можем вершины в этом дереве делать в пространстве любой размерности, то есть в каждой вершине учитывать текущее направление машины, текущую скорость, ускорение, все углы, которые нам важны. А потом, когда мы возьмем новую точку, то возьмем и ближайшую к этой точке вершину. Проедем с помощью какой-то симуляции, например, 5 метров в сторону этой точки. Затем возьмем другую точку и проедем в ее сторону.

Что нам это дает? Мы каждый раз исследуем пространство, но очень агрессивно. Мы не ищем оптимальные способы объехать препятствие. Мы просто ездим в разные стороны, но каждый раз делаем это из наиболее исследуемого участка нашего пространства к той, неизведанной стороне.

Стохастические алгоритмы

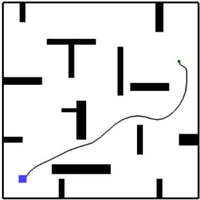
Рис. 5. Один из путей, сгенерированных в процессе построения RRT[8]

Самым распространенным стохастическим алгоритмом является построение быстро исследующего случайного дерева (Rapidly-exploring Random Tree, RRT) или деревьев на его основе (RRT* и прочие).

Принцип заключается в итеративном построении дерева. На каждой итерации происходят следующие действия:

  1. Выбор случайной точки пространства.
  2. Нахождения ближайшего к этой точке узла уже построенного дерева.
  3. Построение ребра в сторону новой точки с помощью симуляции проезда нескольких метров.

За счет этого мы довольно быстро получаем картину, где в разные стороны распространяются пути, которые как-то покрывают наше пространство. Возможно, неоптимально, но довольно быстро. Квадратик в углу — наша стартовая позиция. Потом мы можем получить какой-то путь к цели, который выглядит, возможно, не совсем оптимально, но зато получен достаточно быстрым способом.

Преимущества:

  • Высокая скорость работы в пространствах большой размерности.
  • Пути можно подавать практически напрямую в управляющий блок.

Недостатки:

  • Отсутствие гарантий на оптимальность.
  • Высокая вероятность того, что траектория движения будет сильно извилистой (зависит от выбора дерева; например, RRT* не обладает такой проблемой).

Специализированные алгоритмы

В городе нет абстрактных точек А и Б и неструктурированного окружения со случайными препятствиями. На такого рода сценах все более-менее понятно: есть конкретные полосы и движение машины почти всегда заключается в том, что автомобиль едет примерно по центру полосы, иногда смещается левее или правее, чтобы объехать препятствие, иногда перестраивается, чтобы по правилам дорожного движения повернуть туда, куда нужно.

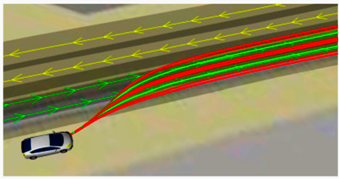
Рис. 6. Построение и выбор плавной траектории смещения[8]

Не всегда нужны хитрые деревья, чтобы парковаться или делать сложные маневры. Когда автомобиль едет на полосе, ему достаточно построить более-менее плавную траекторию, следующую к центру этой полосы или с каким-то смещением влево-вправо. Это сделать гораздо проще, чем искать абстрактный путь в графе. Поэтому простым решением будет взять текущее положение машины, посмотреть на путь, по которому мы хотели бы ехать, и плавно свернуть на этот путь.

Области применения решений проблемы планирования движения

  • Роботизированная хирургия — хирургия с использованием робота во время операции. Поскольку один из способов проведения такого рода операций — автоматический, возникает необходимость решения проблемы планирования движения робота.
  • Компьютерная анимация — вид трехмерной анимации, создаваемый при помощи трёхмерной компьютерной графики. Процедурная анимация полностью или частично рассчитывается компьютером, например:
    • Симуляция физического взаимодействия твёрдых тел.
    • Имитация движения систем частиц, жидкостей и газов.
    • Имитация взаимодействия мягких тел (ткани, волос).
    • Расчёт движения иерархической структуры связей (скелета персонажа) под внешним воздействием.
    • Имитация автономного движения персонажа.
  • Фолдинг белка — процесс спонтанного свертывания полипептидной цепи в уникальную нативную пространственную структуру. Механизм сворачивания белков до конца не изучен, но аминокислотная последовательность белка обычно известна. Поэтому учёные пытаются использовать различные биофизические методы, чтобы предсказать пространственную структуру белка.

См. также

into the abyss

Примечания

  1. ↑ 1,0 1,1 Казаков К.А. и Семенов В.А. (2016) "Обзор современных методов планирования движения"
  2. ↑ Peter Ondruska and Sammy Omari (2020) "The Next Frontier in Self-Driving: Using Machine Learning to Solve Motion Planning"
  3. ↑ Lichuan Deng, Da Li and Ruifang Li (2020) "Improved IMM Algorithm based on RNNs"
  4. ↑ Stefan Becker, Ronny Hug, Wolfgang Hübner, and Michael Arens (2019) "An RNN-based IMM Filter Surrogate"
  5. ↑ Nemanja Djuric, Vladan Radosavljevic, Henggang Cui, Thi Nguyen, Fang-Chieh Chou, Tsung-Han Lin, Nitin Singh, Jeff Schneider (2020) "Uncertainty-aware Short-term Motion Prediction of Traffic Actors for Autonomous Driving"
  6. ↑ Henggang Cui, Thi Nguyen, Fang-Chieh Chou, Tsung-Han Lin, Jeff Schneider, David Bradley, Nemanja Djuric (2020) "Deep Kinematic Models for Kinematically Feasible Vehicle Trajectory Predictions"
  7. ↑ Mustafa Ozan Tezcan (2017) "Motion Estimation Using Convolutional Neural Networks"
  8. ↑ 8,0 8,1 8,2 8,3 Клюев Л. (2017) "Алгоритмы построения пути для беспилотного автомобиля. Лекция Яндекса", Хабр

Источники информации

Источник — «http://neerc.ifmo.ru/wiki/index.php?title=Задача_планирования_движения&oldid=79700»