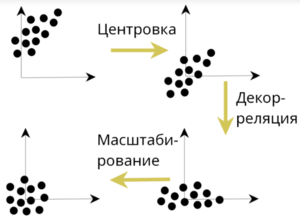
Базовые методы нормализации данных
Применяются независимо к столбцу X
Важно в sklearn.preprocessing есть метод normalize, но это не то, что нам нужно, он рассматривает нормализацию с геометрической точки зрения
(представляет объект в виде вектора), а не по столбцам
Минмакс, [0;1] масштабирование
[math] x_{new} = \dfrac{x_{old} - \min[X]}{\max[X] - \min[X]}[/math]
После нормализации: [math]\min[X_{new}] = 0[/math] и [math]\max[X_{new}] = 1[/math]
Стандартизация, Z-масштабирование
[math] x_{new} = \dfrac{x_{old} - \mathbb{E}[X]}{\mathbb{D}[X]}[/math]
После нормализации: [math]\mathbb{E}[X_{new}] = 0[/math] и [math]\mathbb{D}[X_{new}] = 1[/math]
Декорреляция
1. Есть матрица X.
2. Матрицу центрировали ([math]\mathbb{E}[X_j] = 0[/math]).
3. Ковариация вычисляется по следующей формуле:
[math]\Sigma(X) = \dfrac{1}{N}X^TX[/math]
4. Если же матрица нормализована так, что [math]\mathbb{D}[X_j] = 1[/math], то из произведения мы получим не ковариационную, а корреляционную матрицу
5. Декорреляция вычисляется по формуле:
[math]\hat{X} = X \times \sum^{-1/2}(X)[/math]
где [math]\Sigma^{1/2}[/math] находится из разложения Холецкого
| Утверждение: |
После декорреляции: [math]\sum(\hat{X}) = I[/math] |
| [math]\triangleright[/math] |
|
[math]\Sigma = \dfrac{X^TX}{n}[/math]
[math]\hat{X} = X \times \Sigma^{-1/2}[/math]
[math]\dfrac{\hat{X}^T\hat{X}}{n} = \dfrac{(X * \Sigma^{-1/2})^T * (X * \Sigma^{-1/2})}{n} = \dfrac{\Sigma^{-T/2} * X^T * X * \Sigma^{-1/2}}{n} =
= (\Sigma^{-T/2} * \Sigma^{T/2})*(\Sigma^{1/2}*\Sigma^{-1/2}) = I * I = I[/math]. |
| [math]\triangleleft[/math] |