Предварительная обработка данных
Содержание
Типизация признаков
Преобразование числа
Обычно с числами довольно удобно работать и преобразовывают их достаточно редко.
Дискретизация
- Преобразование в порядковый признак. (берём в числах диапазоны и диапазонам сопоставляем категории)
- Преобразование в категориальный признак. (НО теряется информация о порядке)
Преобразование порядкового типа
- Преобразование в число(берём его порядковый номер)
- Преобразование в k бинарных категорий(если число значений конечно и равно k):
{} - множество значений порядкового признака.(см. рис1)
Преобразование категории
- Бинарную категорию можно преобразовать в число: или
- Категорию из k значений {} можно бинаризовать получив k бинарных категорий:(см. рис2)(НО обратное преобразование иногда невозможно(получим много true и не понятно, к какой категории относить))
- One-hot encoding - преобразование категорий в числа (0, 1): one-hot
Нормализация данных
Приведение данных всех данных к единому формату. Подробнее читай тут
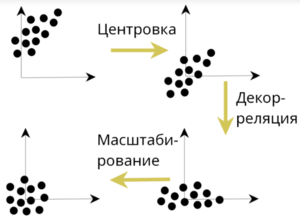
Декорреляция
1. Есть матрица X.
2. Матрицу центрировали ().
3. Ковариация вычисляется по следующей формуле:
4. Если же матрица нормализована так, что , то из произведения мы получим не ковариационную, а корреляционную матрицу
5. Декорреляция вычисляется по формуле:
где находится из разложения Холецкого
| Утверждение: |
После декорреляции: |
|
. |
Аномалии в наборе данных
Аномалии - плохие объекты для построения нашей модели
Задача поиска аномалий является отдельной задачей машинного обучения, про которую можно почитать здесь
Пропуски в наборе данных
Иногда в таблице с данными существую пустоты(они же пропуски), про работу с пропусками можно почитать тут