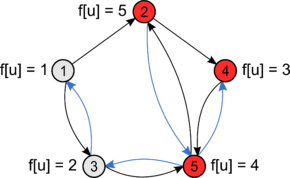
Использование обхода в глубину для поиска компонент сильной связности

Материал из Викиконспекты
Перейти к: навигация, поиск
НЕТ ВОЙНЕ

24 февраля 2022 года российское руководство во главе с Владимиром Путиным развязало агрессивную войну против Украины. В глазах всего мира это военное преступление совершено от лица всей страны, всех россиян.

Будучи гражданами Российской Федерации, мы против своей воли оказались ответственными за нарушение международного права, военное вторжение и массовую гибель людей. Чудовищность совершенного преступления не оставляет возможности промолчать или ограничиться пассивным несогласием.

Мы убеждены в абсолютной ценности человеческой жизни, в незыблемости прав и свобод личности. Режим Путина — угроза этим ценностям. Наша задача — обьединить все силы для сопротивления ей.

Эту войну начали не россияне, а обезумевший диктатор. И наш гражданский долг — сделать всё, чтобы её остановить.

Антивоенный комитет России

Распространяйте правду о текущих событиях, оберегайте от пропаганды своих друзей и близких. Изменение общественного восприятия войны - ключ к её завершению.
meduza.io, Популярная политика, Новая газета, zona.media, Майкл Наки.

Алгоритм

Вершины 2, 4, 5 сильносвязаны.
Синим цветом обозначен обод DFS по инвертированным ребрам

Компоненты сильной связности в графе [math]G[/math] можно найти с помощью поиска в глубину в 3 этапа:

  1. Построить граф [math]H[/math] с обратными (инвертированными) рёбрами
  2. Выполнить в [math]H[/math] поиск в глубину и найти [math]f[u][/math] — время окончания обработки вершины [math]u[/math]
  3. Выполнить поиск в глубину в [math]G[/math], перебирая вершины во внешнем цикле в порядке убывания [math]f[u][/math]

Полученные на 3-ем этапе деревья поиска в глубину будут являться компонентами сильной связности графа [math]G[/math].
Так как компоненты сильной связности [math]G[/math] и [math]H[/math] графа совпадают, то первый поиск в глубину для нахождения [math]f[u][/math] можно выполнить на графе [math]G[/math], а второй — на [math]H[/math].

Доказательство корректности алгоритма

Теорема:
Вершины [math]s[/math] и [math]t[/math] взаимно достижимы [math]\Leftrightarrow[/math] после выполнения алгоритма они принадлежат одному дереву обхода в глубину.
Доказательство:
[math]\triangleright[/math]

[math]\Rightarrow[/math]

Если вершины [math]s[/math] и [math]t[/math] были взаимно достижимы в графе [math]G[/math], то на третьем этапе будет найден путь из одной вершины в другую, это означает, что по окончанию алгоритма обе вершины лежат в одном поддереве.

[math]\Leftarrow[/math]

  1. Вершины [math]s[/math] и [math]t[/math] лежат в одном и том же дереве поиска в глубину на третьем этапе алгоритма. Значит, что они обе достижимы из корня [math]r[/math] этого дерева.
  2. Вершина [math]r[/math] была рассмотрена вторым обходом в глубину раньше, чем [math]s[/math] и [math]t[/math], значит время выхода из нее при первом обходе в глубину больше, чем время выхода из вершин [math]s[/math] и [math]t[/math]. Из этого мы получаем 2 случая:
    1. Обе эти вершины были достижимы из [math]r[/math] в инвертированном графе. А это означает взаимную достижимость вершин [math]s[/math] и [math]r[/math] и взаимную достижимость вершин [math]r[/math] и [math]t[/math]. А складывая пути мы получаем взаимную достижимость вершин [math]s[/math] и [math]t[/math].
    2. Хотя бы одна не достижима из [math]r[/math] в инвертированном графе, например [math]t[/math]. Значит и [math]r[/math] была не достижима из [math]t[/math] в инвертированном графе, так как время выхода [math]r[/math] - больше . Значит между этими вершинами нет пути, но последнего быть не может, потому что [math]t[/math] была достижима из [math]r[/math] по пункту 1).
Значит, из случая 2.1 и не существования случая 2.2 получаем, что вершины [math]s[/math] и [math]t[/math] взаимно достижимы в обоих графах.
[math]\triangleleft[/math]

Время работы алгоритма

  1. Для того, чтобы инвертировать все ребра в графе, представленном в виде списка потребуется [math]O(V + E)[/math] действий. Для матричного представления графа не нужно выполнять никакие действия для его инвертирования.
  2. Количество ребер в инвертированном равно количеству ребер в изначальном графе, поэтому поиск в глубину будет работать за [math]O(V + E)[/math]
  3. Поиск в глубину в исходном графе выполняется за [math]O(V + E)[/math].

В итоге получаем, что время работы алгоритма [math]O(V + E)[/math].

Псевдокод

Пусть [math]G[/math] — исходный граф, [math]H[/math] —инвертированный граф. В массиве [math]ord[/math] будем хранить номера вершин в порядке окончания обработки поиском в глубину в графе [math]G[/math]. В результате получаем массив [math]component[/math], который каждой вершине сопоставляет номер её компоненты. 

   function dfs1(v):                                          
       color[v] = 1
       for (v, u) in E
           if not visited[u]
               dfs1(G[v][u])
       Добавляем вершину v в конец списка ord
   
   function dfs2(v):                                          
       component[v] = col
       for (v, u) in E
           if (вершина u еще не находится ни в какой компоненте)                       
               dfs2(H[v][u])
   
   function main():
       считываем исходные данные, формируем массивы G и H
       for u in V                           
           if not visited[u]
               dfs1(u)
       col = 1
       for (по всем вершинам u списка ord[] в обратном порядке)                                                        
           if (вершина u не находится ни в какой компоненте)
               dfs2(u)
               col++

Источники информации

Источник — «http://neerc.ifmo.ru/wiki/index.php?title=Использование_обхода_в_глубину_для_поиска_компонент_сильной_связности&oldid=83062»