Алгоритм Лампорта-Шостака-Пиза

Алгоритм Лампорта-Шостака-Пиза (1982) решает проблему византийских генералов: если имеется $N$ процессов, среди которых не более $f$ византийских, причём $3f < N$, то они могут прийти к консенсусу за конечное время, используя надёжные каналы связи.

N=4, f=1 с лекции

В первой фазе все процессы шлют своё предложение всем остальным, во второй — пересылают все полученную информацию всем остальным, итого $2N^2$ сообщений.

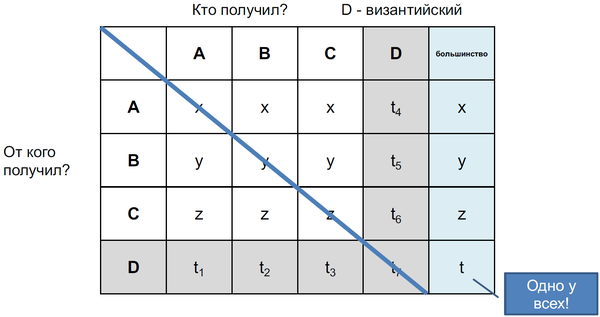
У каждого невизантийского процесса появляется матрица информации: кто кому что сказал. Рассмотрим пример такой матрицы (процесс не знает, какой процесс византийский, мы пометили для демонстрации):

Диагональ вычёркиваем, нам эту информацию и так дали на первой фазе и ей нельзя верить в любом случае (например, так мы вычёркиваем $t_7$, что важно для доказательства ниже).

В столбце византийского процесса находится что угодно, потому что он мог нам сказать что угодно (то есть $t_4$, $t_5$ и $t_6$ могут быть разные у всех процессов). В строчке византийского процесса тоже находится что угодно, но одинаковое для всех процессов, потому что содержимое этой строчки нам гарантированно рассказывают честные процессы (т.е. $t_1$, $t_2$ и $t_3$ одинаковые для всех процессов). Так что большинство в строчке византийского процесса ($t$) непонятное, но одно для всех честных процессов.

А в строчках нормальных процессов находятся константы, за исключением одного столбца от византийского процесса. Таким образом, большинство в каждой строчке (кроме одной византийской) — это то, что соответствующий процесс реально рассылал ($x$, $y$, $z$).

Следовательно, теперь у всех нормальных процессов множество из большинств по строкам одинаковое. Можно применять детерминированную функцию для выбора консенсуса. То есть византийский процесс не может помешать достигнуть консенсуса, но иногда может его изменить.

Идея общего случая с $f>1$

Надо сделать ещё несколько стадий. На первой рассылаем значения, на второй — матрицы, на третьей — кубики (мне прислали такую матрицу), и так далее. На экзамене подробнее не требуется.

Впрочем, описание в Garg (секция 15.4.2, страница 244) требует $N > 4f$, а не $N > 3f$.

Общий случай из старых конспектов

Считаем, что у процессов есть номера. Процесс 1 - "генерал" - рассылает всем предложение - 0 или 1. И после этого молчит (принимает своё предложение).

При f=0 все остальные ("лейтенанты") просто принимают предложение.

При f=1 все "лейтенанты" рассылают всем "лейтенантам" сообщение "генерал сказал X". Теперь у каждого процесса есть N-1 сообщение вида "A сказал, что генерал сказал X", включая своё(Я сказал, что генерал сказал X). Выбираем вариант, который встречается больше раз, или 0 если одинаково. Если сбойный процесс - генерал, то все остальные процессы получат одинаковое количество 0 и 1 в сообщениях и выберут одинаковый вариант. Если сбойный процесс - лейтенант, все остальные процессы получат больше верных сообщений, чем неверных и выберут вариант, посланный генералом.

При f=2+ делаем всего f раундов рассылки сообщений между лейтенантами (при f=2 посылаются сообщения "B сказал, что A сказал, что генерал сказал X"), и f раундов выбора большинства внутри каждого процесса (т.е. для f=2 процесс имеет N-1 сообщение "B сказал, что А сказал ..." и решает, что именно сказал A выбором варианта, который больше встречается).

Если же все процессы равноправные, то в 0 раунде рассылки все считают себя "генералами", а потом делаем консенсус на исходных значениях каждого.

Выбор варианта в конечном итоге даст правильный вариант именно потому, что N > 3f.