Алгоритм поиска подстроки в строке с помощью суффиксного массива

Рассмотрим такую задачу: у нас есть образец [math] p [/math], строка [math] s [/math], суффиксный массив [math] array [/math], построенный для строки [math] s [/math]. Необходимо найти все вхождения образца [math] p [/math] в строку [math] s [/math].

Для наглядности рассмотрим такой пример: образец [math] iss [/math], строка [math] mississippi [/math].
Вот суффиксный массив для данной строки:

#	суффикс	номер суффикса
1	i	11
2	ippi	8
3	issippi	5
4	ississippi	2
5	mississippi	1
6	pi	10
7	ppi	9
8	sippi	7
9	sissippi	4
10	ssippi	6
11	ssissippi	3

Способы поиска

Простейший поиск подстроки

Простейший способ узнать, встречается ли образец в тексте, используя суффиксный массив, это взять первый символ образца и бинарным поиском по суффиксному массиву (массив у нас отсортирован) найти диапазон с суффиксами, начинающимися на такую же букву. Так как все элементы в полученном диапазоне отсортированы, а первые символы одинаковые, то оставшиеся после отбрасывания первого символа суффиксы тоже отсортированы. А значит, можно повторять процедуру сужения диапазона поиска уже по второму, затем третьему и так далее символу образца до получения либо пустого диапазона, либо успешного нахождения всех символов образца. Бинарный поиск работает за [math] O(log|s|) [/math], а сравнение суффикса с образцом не может превышать длины образца. Таким образом время работы алгоритмы [math] O(|p|log|s|)[/math].
В примере поиск будет выглядеть так:

образец	iss	iss	iss
	i	i	i
	ippi	ippi	ippi
	issippi	issippi	issippi
	ississippi	ississippi	ississippi
	mississippi	mississippi	mississippi
	pi	pi	pi
	ppi	ppi	ppi
	sippi	sippi	sippi
	sissippi	sissippi	sissippi
	ssippi	ssippi	ssippi
	ssissippi	ssissippi	ssissippi

Как видно из примера образцу удовлетворяют суффиксы 3 и 4, начинающиеся на 5 и 2 позициях в строке соответственно.

Псевдокод

Поиск диапазона

/*p - образец
n - длина образца
left - левая граница диапазона // изначально равна единице
right - правая граница диапазона // изначально равна длине строки
lh - вспомогательная переменная для определения левой границы диапазона  
rg - вспомогательная переменная для определения правой границы диапазона
find - функция уточнения диапазона
элементы строк и массивов нумеруются с единицы*/
for i = 1 to n {
  lh = n + 1
  rh = 0
  find(left, right, i)
  left = lh
  right = rh
}
if (left != 0 && right != n + 1) { // если диапазон не пуст
  yield left // вывод левой границы диапазона 
  yield right // вывод правой границы диапазона
} else
 yield "No matches" // вывод информации об отсутствии вхождений

Бинарный поиск для уточнения диапазона - функция find(l, r, k)

/*l - левая граница диапазона при поиске
r - правая граница диапазона при поиске
k - номер символа образца, с которым происходит проверка на данном шаге
s - строка
length - длина строки
array - суффиксный массив
x - индекс, стоящий по середине между l и r*/
if (l > r)
  return
x = (l + r) / 2
if (array[x] + k - 1 <= length){
  if (s[array[x] + k - 1] == p[k]){
    if (x < lh)
      lh = x
    if (x > rh)
      rh = x
    find(l, x - 1, k)
    find(x + 1, r, k)
  } else { 
  if (s[array[x] + k - 1] > p[k]) {
    find(l, x - 1, k)
  } else {
  if (s[array[x] + k - 1] < p[k]) {
    find(x + 1, r, k)
  }
} else { 
  find(l, x - 1, k)
  find(x + 1, r, k)
}

Более быстрый поиск

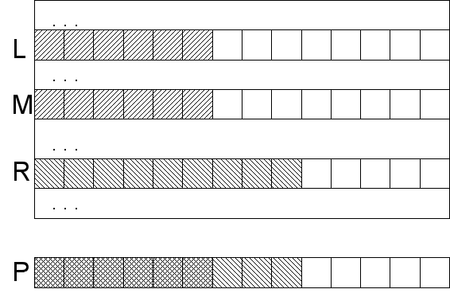
На самом деле нам не обязательно сравнивать всю искомую строку с элементами суффиксного массива. На каждой итерации бинарного поиска мы уточняем некий диапазон, внутри которого может находиться искомый элемент. Все строки в таком диапазоне в некотором смысле похожи. А именно, у данных строк может быть общий префикс с искомой строкой, так как у тех, что остались вне диапазона, общего префикса уж точно не будет (в том смысле, что мы не рассматриваем уже обработанную часть образца как часть префикса).

Пусть границы нашего диапазона на каком-то шаге - это [math] L [/math] и [math] R [/math]. Допустим мы знаем длину общего префикса образца с краями текущего диапазона: [math] l [/math] - общий префикс образца и левого края, [math] r [/math] - общий префикс образца и правого края, где [math] l = lcp(p, array[L]) [/math], [math] r = lcp(p, array[R]) [/math] (lcp - longest common prefix). Будем поддерживать [math] l [/math] и [math] r [/math] после каждого уточнения границ диапазона. Тогда справедливо сделать пару утверждений.
Первое утверждение заключается в том, что для любой строки внутри диапазона lcp не меньше, чем минимум из [math] l [/math] и [math] r [/math]. Если бы это было не так, то значит при неизменной начальной части префикса была бы позиция, где символ сначала совпадал бы с соответствующим символом образца, потом не совпадал, а потом снова совпадал. Это противоречило бы отсортированности диапазона. Важно хорошо проникнуться этой идеей, так как дальше мы ее будем использовать как нечто само собой разумеющееся.
Второе утверждение очевидно: если общий префикс образца и любой строки внутри диапазона не меньше [math] m = min(l,r) [/math], то [math] m [/math] символов можно пропускать сразу, зная, что они совпадают в любом случае, и сравнивать только начиная с [math] m + 1 [/math] символа.

Таким образом мы применим оптимизированное сравнение строк в бинарном поиске строки «в лоб». В худшем случае, конечно, ничего мы от этого не выиграем: если искомый элемент находится на краю массива, но соседи совсем не похожи по [math] lcp [/math], то [math] r [/math] (или [math] l [/math]) будет мало каждый раз, [math] m [/math] будет тоже мало, что сведет оптимизацию на нет. Таким образом в наихудшем случае результат будет прежним [math] O(|p|ln|s|) [/math], но в среднем [math] O(|p| + ln|s|) [/math].