Теорема о существовании простого цикла в случае существования цикла
Версия от 19:18, 4 сентября 2022; Maintenance script (обсуждение | вклад) (rollbackEdits.php mass rollback)
| Лемма: |
Наличие двух различных рёберно простых путей между какими-либо двумя вершинами неориентированного графа равносильно наличию цикла в этом графе. |
| Доказательство: |
|
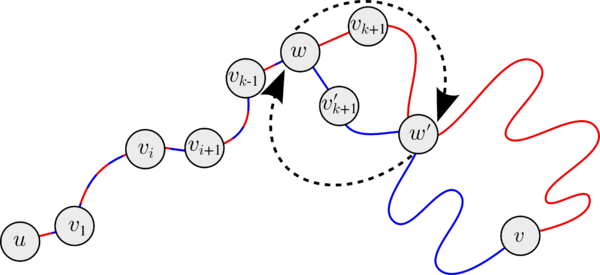
Предположим, что в графе существует два различных рёберно простых пути между вершинами и . Пусть это будут пути и . Пусть их наибольший общий префикс заканчивается в вершине . Заметим, что , т.к. пути различны. Рассмотрим суффиксы путей и : и соответственно. Найдём первую совпадающую вершину в и , не равную . Осталось заметить, что замкнутый путь , полученный объединением части пути вместе с частью цепи , является циклическим путем. Действительно, в путях и двух одинаковых рёбер подряд не бывает, т.к. это рёберно простые пути, а рёбра, смежные с и , не совпадают по построению. Циклический путь является представителем некоторого цикла в графе . Предположим, что в графе существует цикл и пусть циклический путь — его представитель. Найдём первую точку пересечения с самим собой. Такая точка существует, т.к. путь замкнутый. Рассмотрим циклический путь : он простой, т. к. если это неверно и существует вершина , то в вершина повторяется раньше, чем . Теперь элементарно взяв две вершины и легко заметить, что существует два различных рёберно непересекающихся пути между ними: и . |
| Теорема: |
Если в неориентированном графе существует цикл, то в этом графе существует простой цикл. |
| Доказательство: |
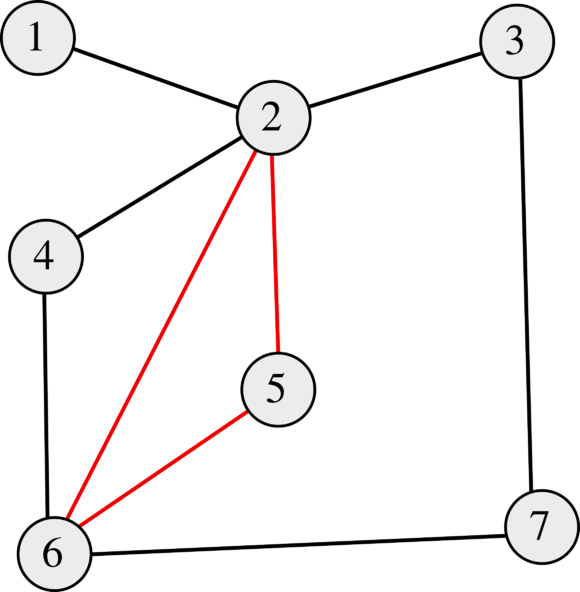
| Выберем в графе минимальный по количеству рёбер цикл (он существует, потому что количество рёбер в любом цикле — натуральное число [1]). Предположим, что он не простой. Но тогда он содержит дважды одну и ту же вершину, т. е. содержит в себе цикл меньшего размера, что противоречит тому, что наш цикл минимальный. Таким образом, этот цикл — простой. |
Замечания
- Так как вершинно-простой путь всегда является рёберно-простым, первая теорема справедлива и для вершинно-простых путей (усиление условия).
- Так как вершинно-простой цикл всегда является рёберно-простым, первая теорема справедлива и для рёберно-простого цикла (ослабление результата).
| Утверждение (неверное): |
Если две вершины графа лежат на цикле, то они лежат на простом цикле. |
| В общем случае неверно, так как эти вершины могут лежать в разных компонентах вершинной или рёберной двусвязности: все пути из одной вершины в другую будут содержать одну и ту же точку сочленения или один и тот же мост. |