Пересечение многоугольников (PSLG overlaying)
Содержание
Введение
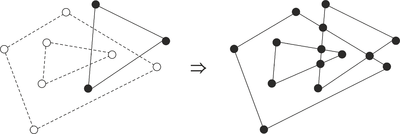
Пересечением двух ППЛГ является ППЛГ, получающийся наложением двух исходных ППЛГ с созданием вершин в точках пересечения ребер. Определим пересечение двух ППЛГ и как ППЛГ , такой, что в нем существует грань тогда и только тогда, когда существуют грани в и в такие, что является наибольшим связным подмножеством . Иначе говоря, пересечение двух ППЛГ — это разбиение плоскости с помощью ребер из и .
| Задача: |
| Необходимо построить РСДС для , имея РСДС для и . Кроме того, для каждой грани из будем хранить ссылки на грани из и , содержащие ее. |
Алгоритм
Для начала скопируем ППЛГ и в новый РСДС. Далее необходимо преобразовать полученный РСДС, чтобы он соответствовал . Отдельно рассмотрим преобразования вершин, полуребер и граней.
Вершины и полуребра
Алгоритм базируется на заметающей прямой, определяющей пересечения отрезков. Запускаем алгоритм на множестве отрезков, представляющих собой ребра из и . Напомним, что алгоритм поддерживает очередь событий и текущий статус заметающей прямой. Также будем поддерживать ссылки между ребрами статуса и соответствующими полуребрами из РСДС. Поддерживаемый инвариант: в любой момент времени РСДС над заметающей прямой корректен.
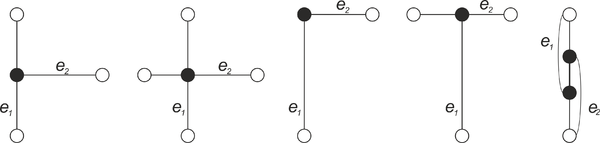
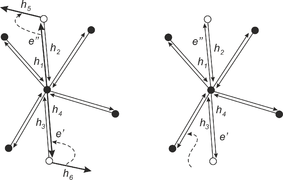
Обработка точки события происходит следующим образом: сначала обновляем и (как в алгоритме пересечения отрезков). Если оба ребра события принадлежат одному ППЛГ, переходим к следующему событию. В противном случае, необходимо модифицировать РСДС. Возможны следующие варианты пересечений (см. рисунок ниже):
- Вершина ребра проходит через ребро , разбивая его на два новых ребра.
- Ребро пересекает ребро . Образуется четыре новых ребра.
- Ребра и пересекаются в общей вершине.
- Вершина ребра проходит через ребро , разбивая его на два новых ребра.
- Ребра и имеют общий отрезок. Образуется новое ребро.
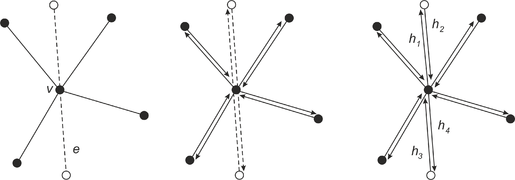
Рассмотрим один из случаев, остальные обрабатываются аналогично. Пусть ребро из проходит через вершину из . Ребро заменяем двумя ребрами и . Два полуребра, соответствующих , заменяются четырьмя полуребрами: два существующих полуребра будут исходить из концов , а два новых полуребра — из (см. рисунок). Устанавливаем ссылки на близнецов для ребер и . Обновим ссылки на следующие полуребра для и , пусть это будут и , соответственно. Не забудем установить полуребра и в качестве предыдущих полуребер у и . Теперь обновим ссылки на полуребра, инцидентные вершине . Для этого сначала при помощи порядка обхода определим, между какими полуребрами находится . Рассмотрим полуребро : свяжем его с первым полуребром, видимым из при обходе по часовой стрелке и исходящем из . Полуребро должно быть связано с первым полуребром, идущим в , при обходе против часовой стрелки. Аналогично обработаем .
Время работы
Большинство шагов алгоритма работают константное время. Определение соседних полуребер с и происходит за линейное время от степени вершины. Следовательно, обновление РСДС не увеличивает время работы алгоритма пересечения отрезков, поэтому сведения о вершинах и полуребрах для итогового РСДС могут быть вычислены за время , где — сумма сложностей и , — количество точек пересечения.
Грани
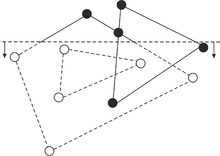
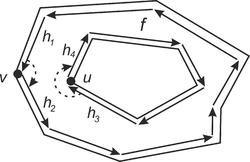
Необходимо получить информацию о гранях итогового РСДС: ссылка на полуребро внешней границы, список ссылок на полуребра дырок внутри грани, ссылка на грани из и , содержащие новую грань. Также необходимо для полуребер установить ссылки на инцидентную грань. У каждой грани существует уникальная внешняя граница, поэтому количество граней будет на единицу больше, чем количество внешних границ (дополнительная граница ограничивает весь ППЛГ). Таким образом, каждой грани можно ставить в соответствие внешнюю границу данной грани (кроме внешней грани ППЛГ, для нее мы введем мнимую внешнюю границу). Следовательно, необходимо обойти все внешние границы ППЛГ и создать грань для каждой границы. Для того, чтобы определить, является цикл внешней границей или дыркой, рассмотрим самую левую вершину цикла (определяется обходом по циклу). Напомним, что полуребра ориентированы так, что инцидентная им грань лежит левее полуребра. С учетом этого, оценим угол внутри грани между полуребрами, инцидентными . Если угол меньше , то цикл является внешней границей грани, в противном случае – лежит внутри грани. Данное свойство выполняется для вершины , но может не выполняться для остальных вершин.
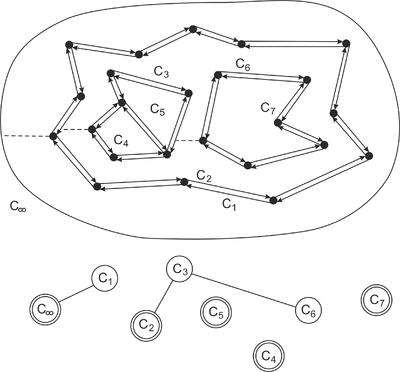
Для определения того, какие границы принадлежат одной грани, построим вспомогательный граф , в котором каждая граница является вершиной. Также добавим вершину для мнимой границы внешней грани. Между двумя вершинами графа, соответствующим двум циклам РСДС, существует ребро тогда и только тогда, когда один цикл является границей дырки, а второй цикл является ближайшим слева к самой левой вершине первого цикла. Если левее самой левой вершины цикла нет полуребер, то соединим этот цикл с мнимой границей внешней грани ППЛГ.
| Лемма: |
Каждой компоненте связности графа соответствует множество циклов, инцидентных только одной грани. |
| Доказательство: |
|
Рассмотрим цикл , ограничивающий дырку в грани . Грань лежит левее самой левой вершины , поэтому должен быть связан с другим циклом грани . Следовательно, циклы одной компоненты связности графа ограничивают одну и ту же грань. Покажем, что каждый цикл, ограничивающий дырку грани , находится в одной компоненте связности с внешней границей грани . Предположим, что существует цикл, для которого это не выполняется. Пусть – самый левый такой цикл, причем его левая вершина также самая левая. По определению, существует ребро между и циклом , который лежит левее . Следовательно, лежит в одной компоненте связности с , причем не является внешней границей . Получается, что лежит левее , что противоречит определению . |
Построение графа
Напомним, что в алгоритме заметающей прямой для пересечения отрезков мы искали ближайший отрезок, находящийся левее точки события. Эта информация необходима для построения графа . Сначала создадим вершину для каждой границы. Далее необходимо построить ребра в графе, для этого найдем левую вершину каждой дырки и определим, какое ребро лежит слева от данной вершины. Для эффективности будем для каждого полуребра хранить ссылку на вершину графа, содержащую это полуребро. Таким образом, информация о гранях может быть восстановлена за время , после алгоритма заметающей прямой. Также заметим, что информацию о структуре графа можно хранить в записях граней.
Маркировка граней
Необходимо для каждой грани РСДС определить, какие грани из и содержат ее. Рассмотрим вершину грани . Если является пересечением ребра из и ребра из , то по указателям на инцидентные грани можно определить, какие грани содержат данные ребра. Если является вершиной , то мы можем определить только грань из , содержащую . Необходимо научиться определять грань из , содержащую . То есть для каждой вершины из мы должны знать, какая грань из содержит данную вершину, и наоборот. Это также делается заметающей прямой.
Итог
Вход: два ППЛГ и , представленные в виде РСДС.
Выход: пересечение и , представленное в виде РСДС .
- Скопируем и в новый РСДС .
- Найдем пересечения ребер из и с помощью заметающей прямой. При обработке события будем обновлять , если событие затрагивает и . Также для вершины события сохраним информацию о ближайшем полуребре слева.
- Найдем граничные циклы в , обходя .
- Построим граф , вершинам которого соответствуют циклы, соединив ребрами дырки и циклы, ближайшие слева к левым вершинам дырок.
- Для каждой компоненты связности графа : пусть – внешняя граница компоненты связности, ограничивающая грань . Создать запись для этой грани, установить ссылку на полуребро внешней границы грани и ссылки на полуребра дырок грани. Также для всех полуребер грани установить ссылки на инцидентную грань.
- Для каждой грани из установить ссылки на грани из и , содержащие .
Общее время работы
| Теорема: |
Пусть имеет сложность , имеет сложность , . Пересечение и может быть построено за время , где – количество точек пересечения и . |
| Доказательство: |
| Копирование двух РСДС в один занимает времени, заметающая прямая работает времени по лемме. Создание граней работает линейное время от сложности . Маркировка граней РСДС работает за . |
См.также
- ППЛГ и РСДС (PSLG и DCEL): определение, построение РСДС множества прямых
- Пересечение множества отрезков
Источники информации
- de Berg, Cheong, van Kreveld, Overmars. Computational Geometry, Algorithms and Applicants, 2008. pp. 33-39