|
Пусть [math]H[/math] — пересечение всех максимальных по включению барьеров графа [math]G[/math]. Чтобы доказать теорему, докажем, что [math]A(G)\subset H[/math] и [math]A(G)\supset H[/math].
[math]A(G)\subset H[/math]:
Пусть [math]B[/math] — максимальный по включению барьер, [math]|A(G)\setminus B| = k \gt 0[/math], [math]B' = B \cup A(G) \Rightarrow |B'| = |B| + k[/math].
Докажем, что [math]B'[/math] — барьер и получим противоречие. Для этого достаточно доказать, что [math]\mathrm{odd}(G\setminus B')\ \geqslant \mathrm{odd}(G\setminus B)\ + k[/math], ведь в таком случае [math]\mathrm{odd}(G\setminus B')\ \geqslant \mathrm{def}(G)\ + |B| + k \Rightarrow \mathrm{odd}(G\setminus B')\ - |B'| \geqslant \mathrm{def}(G)[/math].
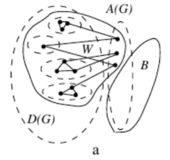
Пусть [math]W[/math] — компонента связности графа [math]G - B[/math], содержащая [math]t \gt 0[/math] вершин из [math]A(G)[/math] (см. рисунок [math]1[/math]), если такой компоненты нет, то [math]k = 0[/math] — противоречие.
В силу леммы о связи барьера с [math]D(G)[/math], [math]B\cap D(G) = \varnothing \Rightarrow B'\cap D(G) = \varnothing[/math]. Поэтому, [math]W[/math] содержит все компоненты связности графа [math]G(D(G))[/math], соединённые рёбрами с [math]W\cap A(G)[/math].
По теореме Эдмондса-Галлаи все эти компоненты связности нечетные и их хотя бы [math]t + 1[/math].
Таким образом, при добавлении [math]t[/math] вершин из [math]W\cap A(G)[/math] в барьер может исчезнуть одна нечётная компонента связности (если [math]|W|[/math] нечётно), а появляется хотя бы [math]t + 1[/math] нечётных компонент связности.
Просуммировав прибавления по всем компонентам связности графа [math]G - B[/math], содержащим вершины из [math]A(G)[/math], мы получим, что [math]\mathrm{odd}(G\setminus B')\ \geqslant \mathrm{odd}(G\setminus B)\ + k[/math], что и требовалось доказать.
[math]A(G)\supset H[/math]:
Предположим противное: пусть существует вершина [math]x\notin A(G)[/math], принадлежащая всем максимальным барьерам. По теореме о структуре барьера [math]x\in C(G)[/math].
Рассмотрим максимальное паросочетание [math]M[/math] графа [math]G[/math], пусть [math]xy\in M[/math].
Докажем, что [math]B = A(G)\cup \{ y \}[/math] — барьер графа [math]G[/math]. Так как [math]|B| = |A(G)| + 1[/math], достаточно доказать, что [math]\mathrm{odd}(B)\ \geqslant \mathrm{odd}(A(G))\ + 1[/math].
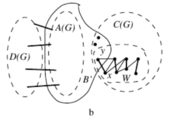
По теореме Эдмондса-Галлаи [math]y\in C(G)[/math]. Пусть [math]W[/math] — компонента связности графа [math]C(G)[/math], содержащая [math]x[/math] и [math]y[/math] (см. рисунок [math]2[/math]). Вершины [math]W[/math] разбиваются на пары соединённых рёбрами из [math]M[/math], поэтому [math]|W|[/math] чётно.
Множество [math]W' = W\setminus \{ y \}[/math] содержит нечётное число вершин и является объединением нескольких компонент связности графа [math] G - B[/math], которых нет в [math]G - A(G)[/math]. Среди этих компонент связности есть нечётная, значит [math]B[/math] — барьер графа [math]G[/math].
Пусть [math]B'[/math] — максимальный барьер графа [math]G[/math], содержащий [math]B[/math].
В максимальном паросочетании [math]M[/math] графа [math]G[/math] все вершины барьера [math]B'[/math] должны быть соединены рёбрами с вершинами различных нечётных компонент связности графа [math]G - B'[/math], следовательно, [math]x\notin B'[/math].
Полученное противоречие показывает, что пересечение всех максимальных барьеров графа [math]G[/math] может содержать только вершины из [math]A(G)[/math]. |