Алгоритм Бентли-Оттмана
Алгоритм Бентли-Оттмана(англ. Bentley-Ottmann) — алгоритм, позволяющий по множеству отрезков на плоскости получить множество точек, в которых эти отрезки пересекаются, при этом для каждой точки алгоритм выдает множество отрезков, пересекающихся в ней.
Постановка задачи
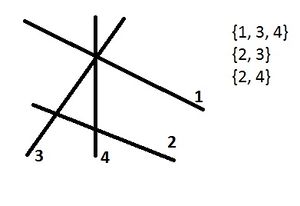
На плоскости лежит отрезков, каждый из них задан координатами своих концов. Требуется по этим данным определить множество точек, в которых эти отрезки пересекаются. Однако, не всегда координаты точки можно абсолютно точно представить с помощью вещественных типов данных. Поэтому характеризовать каждую точку будем множеством отрезков, которые пересекаются в этой точке.
Для упрощения понимания введем три ограничения на входные данные:
- не существует вертикальных отрезков
- не существует пары отрезков, имеющих более одной общей точки
- никакие три отрезка не пересекаются в одной точке
Как обрабатывать эти случаи, будет объяснено позднее.
Алгоритм
Основная идея
Алгоритм будет основан на идее сканирующей прямой. Опишем три типа событий, которые мы и будем обрабатывать:
- начался новый отрезок
- два отрезка пересеклись
- отрезок закончился
Сканирующая прямая будет расположена параллельно оси ординат, и двигаться вдоль оси абсцисс в сторону ее положительного направления. Учитывая введенные ограничения на входные данные, прямая никогда не будет проходить через два события одновременно.
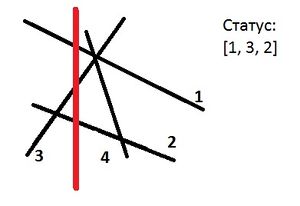
Статус
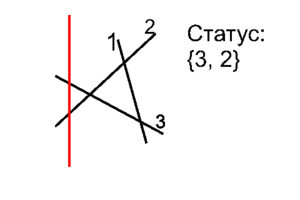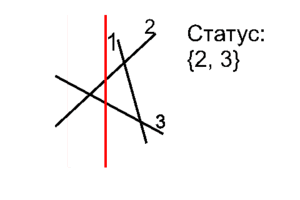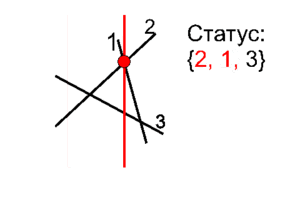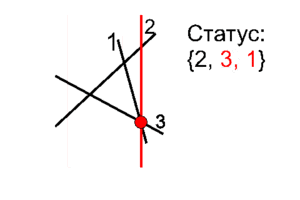
Назовем статусом множество, в котором содержатся все отрезки, пересекающие нашу сканирующую прямую. Важно, что эти отрезки должны быть упорядочены по возрастанию (или убыванию) координаты их пересечения с прямой. Заметим, что в процессе работы алгоритма отрезки могут добавляться в произвольные места этого упорядоченного множества, удаляться из произвольных мест или меняться местами друг с другом.
Важная мысль
Попробуем найти событие, которое случится раньше всех других, если наша прямая уже пересекает какие-то отрезки. Нам, в данный момент, интересен случай, когда это событие является пересечением отрезков. Важно, что в этом пересечении участвуют два отрезка, которые обязательно являются соседними в нашем статусе.
Доказательство
Предположим, что это не так. Значит, между этими двумя пересекающимися отрезками существует еще хотя бы один. Поскольку эти два отрезка пересекаются, то или третий пересекает перед их пересечением один из них, или пересекается с ними в той же точке. В любом случае, Важная мысль верна
В итоге
Изначально у нас есть только события вида "начался отрезок" и "закончился отрезок". События вида "пересекаются два отрезка" будут добавляться нами в множество еще не обработанных событий. Соответственно, алгоритм выглядит так: выбираем то событие из множества необработанных, у которого наименьшая координата , обрабатываем, делаем так, пока множество необработанных событий непустое. Плюс, на протяжении всего алгоритма должен поддерживаться следующий инвариант: в множество необработанных событий уже добавлены все пересечения отрезков, которые в текущем статусе текущие.
Обработка событий
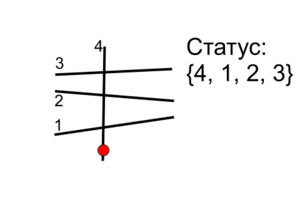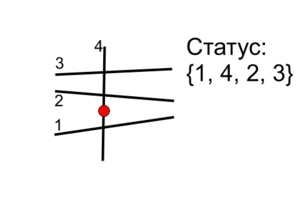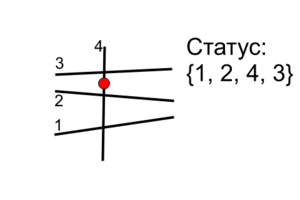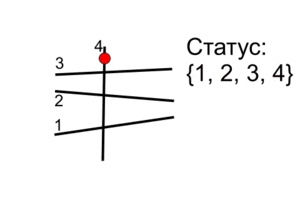
Событие "начало отрезка"
Находим в статусе два отрезка, между которыми будет находится тот, который начинается. После этого добавляем его в статус на это место и точки его пересечения с соседними добавляем в множество необработанных событий.
Событие "конец отрезка"
Находим в статусе отрезок, который заканчивается. Удаляем его оттуда, после чего в множество необработанных событий добавляем точку, в которой пересекаются отрезки, которые были соседями заканчивающегося в старом статусе. Это необходимо, потому что в новом статусе они станут соседними. Заметим, что добавляемое событие может уже находиться в множестве, но нас это совершенно не напрягает.
Событие "пересечение отрезков"
Находим в статусе два отрезка, которые пересекаются. Меняем их местами (это действительно происходит). После этого добавляем в множество пересечения двух новых пар соседей, которые появились после перестановки пересекшихся отрезков.
Обработка "нехороших случаев"
Сканирующая точка
Решим, для начала, вопрос с вертикальными отрезками. Важно, что заодно пропадет и проблема с обработкой событий, имеющих одинаковую координату по оси .
Слегка поменяем нашу концепцию. Сканирующая прямая теперь становится не совсем прямой. Теперь у нас появляется, скорее, сканирующая точка. Суть изменения в следующем: в случае, если несколько событий попадают на одну вертикальную прямую, мы их обрабатываем в порядке возрастания координаты по оси . Внимательный читатель сейчас, наверное, воскликнет: "А как же тогда наш статус? Ведь отрезки не могут пересекать точку!". Однако и это не является проблемой. Если отрезок, который лежит в статусе, не вертикален, то он сортируется по своей координате , в которой он пересекается с вертикальной прямой, проведенной через нашу точку (да, это бывшая сканирующая прямая). А вот если отрезок вертикален, то его параметром является как раз ордината "сканирующей точки". Если внимательно подумать, то все будет корректно.
Несколько отрезков в одной точке
Первый метод решения проблемы
У нас есть упорядоченное множество необработанных событий. Давайте перед добавлением события будем проверять, а нет ли его там. Если оно там уже есть, то события вида "в этой точке перечекаются отрезки и ", превратится в событие вида "в этой точке пересекаются отрезки , и ". В процессе обработки этой точки порядок следования в статусе всех отрезков, пересекающихся в ней, просто инвертируется. Соответственно, проблема решилась.
Второй метод решения проблемы
На самом деле, посмотрим более внимательно, что произойдет в этой точке. Все пересечения всех пар обработаются. Всего таких пар , где в точке пересекается отрезков. Если в некой перестановке делается элементарных транспозиций, и ни одна из них не повторяется, то перестановка становится инвертированной. Так что, даже если оставить все как есть, то все будет работать. Такие дела. Здесь тоже должна быть соответствующая анимашка.
СНМ вместо отрезков
Внимание! Этот раздел должен интересовать только задротов любознательных, так как он описывает разбор случая, который нам, по обещанию Ковалева, не встретится.
Нам остался последний сложный случай: наложение двух или более отрезков друг для друга. Давайте теперь вместо просто отрезков будем класть в СНМ следующее: множество отрезков, которые на данном этапе накладываются друг на друга. Понятно, что при добавлении нового отрезка он или создает свое множество, или добавляется в уже существующее. При удалении удаляется из множества, если оно осталось пустым — удаляется и само множество. А при пересечении с другим множеством попарно пересекаются все отрезки из двух множеств. При этом важно, что все отрезки, накладывающиеся друг на друга, должны занимать в статусе одну ячейку, т. е. являться одним множеством.
Реализация алгоритма
Двоичное дерево поиска в качестве статуса
Из определения статуса ясно, какую структуру удобно использовать в качестве статуса: двоичное дерево поиска. В нем удобно делать все необходимые операции, и выполняться они будут за .
Реализация множества необработанных событий
Приоритетная очередь
Опять же, эта идея возникает в процессе описания этого множества. При этом понятно, что точки сравниваются сначала по абсциссе, в случае равенства — по ординате.
Двоичное дерево поиска
В принципе, вполне себе вариант реализации упорядоченного множества. Но его стоит использовать только тогда, когда мы хотим рассматривать пересечение нескольких отрезков в одной точке в качестве отдельного случая, а не как несколько попарных пересечений. Заметим, что это существенно усложняет реализацию.
Наконец, абсолютная точность
Заметим, что мы не умеем получать абсолютно точные координаты пересечения двух отрезков. Однако, мы умеем представлять эти координаты в качестве суммы произведений нескольких чисел (просто пересечение прямых и раскрытие скобок в верхней части дроби). А сами координаты нам и не требуются, нам необходимо только уметь сравнивать эти координаты друг с другом. Сравнивать же эти суммы произведений с другими такими же суммами и с обычными числами (в обобщенном представлении тоже такими же суммами) мы тоже умеем. Победа!