Материал из Викиконспекты
Числа Эйлера I рода
| Определение: |
| Пусть [math]a[/math] и [math]b[/math] — соседние элементы некоторой перестановки порядка [math]n[/math] причем [math]a \lt b[/math]. Тогда пара [math](a, b)[/math] называется подъемом (англ. ascent) данной перестановки. |
Числа Эйлера I рода (англ. Eulerian numbers) — количество перестановок чисел от [math]1[/math] до [math]n[/math] таких, что в каждой из них существует ровно [math]m[/math] подъемов. Числа Эйлера I рода обозначают как [math]\langle{n\atop m}\rangle [/math] или же [math]A(n, m)[/math].
Вывод рекуррентной формулы
Пусть у нас есть некая перестановка [math] \pi = \pi_1, \pi_2\ldots \pi_{n-1} [/math]. Тогда операцией вставки элемента с номером [math]n[/math] в какую-либо из позиций мы получим [math]n[/math] перестановок вида [math]\theta = \theta_1, \theta_2\ldots \theta_p, n, \theta_q\ldots \theta_{n-1}[/math]. Далее рассмотрим два случая:
- Количество подъемов в перестановке [math]\theta[/math] равно количеству подъемов в [math]\pi[/math]. Этого можно добиться, вставляя элемент [math]n[/math] на самое первое место в [math]\theta[/math] (всего [math]\langle{n - 1\atop m}\rangle [/math] возможностей) или перед последним последним элементом каждого подъема (еще [math]m \times [/math][math] \langle{n - 1\atop m}\rangle [/math] раз).
- Количество подъемов в новой перестановке на один больше предыдущего количества. Этого эффекта добиваемся вставкой элемента [math]n[/math] во все места, не подходящие по критерию первого пункта. Таких вставок, как не трудно догадаться, можно совершить [math](n - m)[/math][math]\langle{n - 1\atop m - 1}\rangle[/math].
Тогда рекуррентная формула имеет вид:
- [math]\left\langle{n\atop m}\right\rangle[/math] [math] = (m + 1)[/math] [math]\left\langle{n - 1\atop m}\right\rangle[/math] [math] + (n - m)[/math] [math]\left\langle{n - 1\atop m - 1}\right\rangle[/math]
Примем также следующее начальное значение:
- [math]\left\langle{0\atop m}\right\rangle[/math] [math] = [m = 0][/math][1].
Пример
Рассмотрим все перестановки порядка [math]4[/math], в которых есть ровно [math]2[/math] подъема (в квадратных скобках один или больше подъемов подряд):
- [math] \left\langle{4\atop 2}\right\rangle[/math] [math] = 11:
[124]3,
[13][24],
[134]2,
[14][23],
2[134],
[23][14],
[23][41],
[24][13],
3[124],
[34][12],
4[123],
[/math]
Согласно алгоритму вывода рекуррентной формулы мы можем добавить [math]4[/math] в следующие позиции всех перестановок порядка [math]3[/math] с двумя подъемами, не увеличив количество подъемов:
- [math]
\left\langle{3\atop 2}\right\rangle[/math] [math] = 1:
[123] \Rightarrow (4)[123], [1(4)][23], [12(4)]3
[/math]
Далее рассмотрим все перестановки порядка [math]3[/math] с одним подъемом, причем операцией вставки [math]4[/math] мы будем увеличивать количество подъемов на [math]1[/math]:
- [math] \left\langle{3\atop 1}\right\rangle[/math] [math] = 4:[/math]
- [math][13]2 \Rightarrow [13(4)]2, [13][2(4)];[/math]
- [math]2[13] \Rightarrow [2(4)][13], 2[13(4)];[/math]
- [math][23]1 \Rightarrow [23(4)]1, [23][1(4)];[/math]
- [math]3[12] \Rightarrow [3(4)][12], 3[12(4)];[/math]
Таким образом мы убеждаемся в верности формулы:
- [math] \left\langle{4\atop 2}\right\rangle[/math] [math] = (2 + 1)[/math] [math]\left\langle{3\atop 2}\right\rangle[/math] [math] + (4 - 2)[/math] [math]\left\langle{3\atop 1}\right\rangle[/math] [math] = 11;[/math]
Треугольник чисел Эйлера I рода
На значениях [math]n = m[/math] чисел Эйлера I рода можно построить массив [math]n \times m[/math], нижнедиагональная часть которого названа треугольником чисел Эйлера I рода.
|
|
m = 0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
| n = 0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
| 1
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
| 2
|
1
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
| 3
|
1
|
4
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
| 4
|
1
|
11
|
11
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
| 5
|
1
|
26
|
66
|
26
|
1
|
0
|
0
|
0
|
0
|
0
|
| 6
|
1
|
57
|
302
|
302
|
57
|
1
|
0
|
0
|
0
|
0
|
| 7
|
1
|
120
|
1191
|
2416
|
1191
|
120
|
1
|
0
|
0
|
0
|
| 8
|
1
|
247
|
4293
|
15619
|
15619
|
4293
|
247
|
1
|
0
|
0
|
| 9
|
1
|
502
|
14608
|
88234
|
156190
|
88234
|
14608
|
502
|
1
|
0
|
Явные формулы
- [math]\left\langle{n\atop m}\right\rangle[/math] [math] = \sum\limits_{j=1}^{m+1} (-1)^{m-j+1} {n+1\choose m-j+1}j^{n}[/math]
- [math]\left\langle{n\atop m}\right\rangle[/math] [math] = \sum\limits_{j=0}^{m}(-1)^j {n+1\choose j} (m+1-j)^n[/math]
Связь чисел Эйлера I рода с сечениями гиперкубов
| Теорема: |
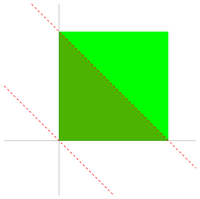
Число [math]\dfrac{1}{n!}[/math] [math]\left\langle{n\atop m}\right\rangle[/math] выражает объем части [math]n[/math]-мерного единичного гиперкуба, ограниченного гиперплоскостями [math]x_1+x_2+\dots+x_n=m[/math] и [math]x_1+x_2+\dots+x_n=m-1[/math]. |
| Доказательство: |
| [math]\triangleright[/math] |
|
Для доказательства этого факта нам потребуется следующая теорема:
| Теорема (Об объемах сечений [math]n[/math]-мерных гиперкубов полупространствами): |
Пусть [math]w \in \mathbb{R}[/math] — вектор с ненулевыми компонентами ( [math]w = {w_1, w_2 \ldots w_n}[/math]), а [math]z \in \mathbb{R}_+[/math]. Тогда верно следующее равенство:
[math]\mathrm{Vol}_{n}(G^n_{w,z} \cap I^{n}) = \dfrac{1}{n! \prod\limits_{i=1}^{n}w_i} \sum\limits_{K \subseteq [n]} (-1)^{|K|}(z-w \cdot 1_K)^n_+[/math]
- [math]G_{w, z}^{n} := \{x \in \mathbb{R}^{n} : (w \cdot x) \leqslant z \}[/math] — полупространство;
- [math]I^n := [0,1]^n[/math];
- [math][n] := \{1,2\ldots n\}[/math];
- [math]1_K[/math], где [math]K[/math] — подмножество [math]\{1,2\ldots n\}[/math], — вектор, где значения координат с номерами, входящими в [math]K[/math], равны [math]1[/math], а остальные — нули;
- Для [math]r \in \mathbb{R}[/math] и [math]n \in \mathbb{N}[/math] : [math]r^n_+ := (\max{\{r, 0\}})^n[/math].
|
| Доказательство: |
| [math]\triangleright[/math] | |
С доказательством можно ознакомиться по ссылке [2]. | | [math]\triangleleft[/math] |
Рассмотрим пересечение гиперкуба полупространством [math]G^n_{1_{[n]},m}[/math]. Вектор [math]1_{[n]}[/math] (все координаты которого равны единицы) появляется здесь ввиду того, как мы определили в формулировке секущие гиперплоскости ([math]x_1+x_2+\ldots +x_n = m | m+1[/math]) — это вектор нормали к [math]\mathrm{G}[/math]. Очевидно, что при данном значении вектора произведение [math]\prod\limits_{i=1}^{n}w_i[/math] равно единице (вектор [math]w_i[/math] тут — единичный вектор [math]1_{[n]}[/math], то есть рассматривается произведение всех его координат — единиц). Рассмотрим выражение, стоящее под знаком суммы. При итерации по подмножествам [math][n][/math] равной мощности будут получаться одинаковые слагаемые, так как выражение [math](-1)^{|K|}(z-w \cdot 1_K)^n_+[/math] зависит лишь от мощности итерируемого в сумме подмножества [math]K[/math] — скалярное произведение [math]w \cdot 1_K[/math] одинаково за счет того лишь факта, что оно вычисляется как сумма произведений соответствующих координат, где ровно [math]n - |K|[/math] их обращаются в ноль. Такое скалярное произведение будет равно мощности [math]K[/math]. Заменим итератор суммы значением мощности множества [math]K[/math]. Также ограничим верхний индекс суммирования значением [math]m+1[/math], так как при больших значениях [math]j[/math] слагаемое будет обращаться в ноль ([math]r^n_+[/math]). Отсюда имеем [math]{n \choose j}[/math] таких одинаковых слагаемых, где [math]j = |K|[/math].
Тогда перейдем от первоначальной формулировки теоремы к следующей:
- [math]\mathrm{Vol}_{n}(G^n_{1_{[n]},m} \cap I^{n}) = \dfrac{1}{n!}\sum\limits_{j = 0}^{m + 1} (-1)^{j}{n \choose j}(m-j)^n[/math]
Положим [math]W_n^m[/math] — фигура, образованная сечением гиперкуба [math][0,1]^{n}[/math] плоскостями [math]\sum\limits_{i=1}^{n} x_{i} = m[/math] и [math]\sum\limits_{i=1}^{n} x_{i} = m+1[/math].
- [math]W_n^m := \{ x \in \mathbb{R} : m \leqslant x \cdot 1_{[n]} \leqslant m+1 \} \cap I^{n}[/math]
Тогда перейдем к следующему равенству:
- [math]\mathrm{Vol}_{n}(W_n^m) = \mathrm{Vol}_n(G_{1_{[n]},m+1}^{n} \cap I^n) - \mathrm{Vol}_n(G_{1_{[n]},m}^{n} \cap I^n)[/math]
- [math]= \dfrac{1}{n!}[\sum\limits_{j=0}^{m+1}(-1)^{j}{n \choose j}(m+1-j)^{n} - \sum\limits_{j=0}^{m}(-1)^{j}{n \choose j}(m-j)^{n}][/math]
- [math] = \dfrac{1}{n!}\sum\limits_{j=0}^{m+1}(-1)^j{n+1 \choose j}(m+1-j)^n[/math]
- [math] = \dfrac{1}{n!}\sum\limits_{j=0}^{m}(-1)^j{n+1 \choose j}(m+1-j)^n[/math] (элемент суммы с номером [math]j=m+1[/math] обращается в ноль)
- [math] = [/math] [math]\dfrac{1}{n!}[/math] [math]\left\langle{n\atop m}\right\rangle[/math] (вторая явная формула)
|
| [math]\triangleleft[/math] |
Свойства
- Нетрудно увидеть, что каждый ряд ненулевых значений симметричен относительно своей середины, то есть:
- [math]\left\langle{n\atop m}\right\rangle = \left\langle{n\atop (n-1) - k}\right\rangle[/math][math],\ n \geqslant 1,\ 0 \leqslant k \leqslant n-1. \, [/math]
- Сумма всех значений каждого ряда равна [math] n! [/math]:
- [math]\sum\limits_{m=0}^{n}[/math][math] \left\langle{n\atop m}\right\rangle[/math] [math] = n!,\ n \geqslant 0, \,[/math]
- Связь чисел Эйлера I рода с числом сочетаний:
- [math]\sum\limits_{m=0}^n (-1)^m [/math][math]{\left\langle{n\atop m}\right\rangle}[/math] [math]{n-1\choose m}^{-1}=0.[/math]
- Вероятность того, что сумма [math]n[/math] независимых равномерно распределённых в отрезке [math][0,1][/math] переменных лежит между [math]m-1[/math] и [math]m[/math] равна [math]\dfrac{1}{n!}\left\langle{n\atop m}\right\rangle[/math].
Числа Эйлера II рода
Числа Эйлера II рода (англ. Eulerian numbers of the second kind) — количество перестановок мультимножества от [math]1[/math] до [math]n[/math] вида [math]\{1,1,2,2\ldots n,n\}[/math], обладающих свойством "все элементы перестановки, встречающиеся между двумя вхождниями [math]z[/math] для любого [math]z[/math], больше, чем [math]z[/math]", таких, что в каждой из них существует ровно [math]m[/math] подъемов. Числа Эйлера II рода обозначаются как [math] \scriptstyle \left\langle \!\! \left\langle {n \atop m} \right\rangle \!\! \right\rangle [/math]
Пример
Рассмотрим [math] n = 3[/math]. Тогда существует [math]15[/math] перестановок такого вида, среди которых одна не имеет подъемов, [math]8[/math] штук имеют всего [math]1[/math] подъем, и [math]6[/math] перестановок имеют [math]2[/math] подъема:
- [math] 332211,\; [/math]
- [math] 221[13]3,\; 22[13]31,\; 2[23]311,\; [23]3211,\; 1[13]322,\; [13]3221,\; 331[12]2,\; 33[12]21, [/math]
- [math]1[12][23]3,\; [12]2[13]3,\; 1[123]32,\; [123]321,\; [13]3[12]2,\; [12][23]31. [/math]
| Лемма: |
Количество перестановок мультимножества [math]\{1,1,2,2\ldots n,n\}[/math] со свойством "все элементы перестановки, встречающиеся между двумя вхождниями [math]z[/math] для любого [math]z[/math], больше, чем
[math]z[/math]" равно двойному факториалу [math](2n-1)!![/math]. |
| Доказательство: |
| [math]\triangleright[/math] |
|
Докажем лемму методом математической индукции.
- База. Для [math]n=1[/math] очевидно, что существует только одна такая перестановка.
- Переход. Рассмотрим какую-нибудь перестановку длины [math]2n[/math]. Таких перестановок [math](2n-1)!![/math]. Теперь докажем, что перестановок длины [math]2(n+1)[/math] будет [math](2(n+1)-1)!![/math]. Попробуем вставить два числа [math]n + 1[/math]. Очевидно, что их нельзя вставить не на соседние места, так как в таком случае между ними точно будут меньшие элементы. Но их можно вставить в любые два соседних места, так как они больше всех чисел в перестановке, а значит они не нарушат свойства для других элементов. Таким образом два новых элемента можно вставить в [math]2n+1[/math] место. В итоге перестановок длины [math]2(n+1)[/math] будет [math](2n-1)!!\cdot (2n+1)=(2n+1)!!=(2(n+1)-1)!![/math].
|
| [math]\triangleleft[/math] |
Рекуррентная формула
Числа Эйлера II рода можно выразить рекурсивно следующим образом:
- [math] \left\langle \!\! \left\langle {n \atop m} \right\rangle \!\! \right\rangle[/math] [math] = (2n-m-1) [/math] [math]\left\langle \!\! \left\langle {n-1 \atop m-1} \right\rangle \!\! \right\rangle[/math] [math] + (m+1) [/math] [math]\left\langle \!\! \left\langle {n-1 \atop m} \right\rangle \!\! \right\rangle, [/math]
С начальным условием для [math]n = 0[/math]:
- [math] \left\langle \!\! \left\langle {0 \atop m} \right\rangle \!\! \right\rangle[/math] [math] = [m=0]. [/math]
Треугольник чисел Эйлера II рода
Значения чисел Эйлера II рода для [math]0 \leqslant n \leqslant m \leqslant 9[/math] представлены в данном массиве. Нижнедиагональная его часть называется треугольником чисел Эйлера II рода.
|
|
m = 0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
| n = 0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
| 1
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
| 2
|
1
|
2
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
| 3
|
1
|
8
|
6
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
| 4
|
1
|
22
|
58
|
24
|
0
|
0
|
0
|
0
|
0
|
0
|
| 5
|
1
|
52
|
328
|
444
|
120
|
0
|
0
|
0
|
0
|
0
|
| 6
|
1
|
114
|
1452
|
4400
|
3708
|
720
|
0
|
0
|
0
|
0
|
| 7
|
1
|
240
|
5610
|
32120
|
58140
|
33984
|
5040
|
0
|
0
|
0
|
| 8
|
1
|
494
|
19950
|
195800
|
644020
|
785304
|
341136
|
40320
|
0
|
0
|
| 9
|
1
|
1004
|
67260
|
1062500
|
5765500
|
12440064
|
11026296
|
3733920
|
362880
|
0
|
См. такжеПримечанияИсточники информации