Алгоритм двух китайцев
Алгоритм двух китайцев — алгоритм построения минимального остовного дерева во взвешенном ориентированном графе с корнем в заданной вершине. Был разработан математиками Чу Йонджином и Лю Цзенхонгом.
Постановка задачи
Дан взвешенный ориентированный граф и начальная вершина . Требуется построить корневое остовное дерево в с корнем в вершине , сумма весов всех ребер которого минимальна.
Алгоритм
Описание
Если хотя бы одна вершина графа недостижима из , то требуемое дерево построить нельзя.
|
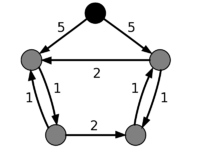
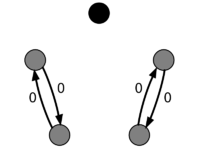
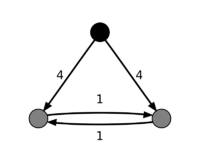
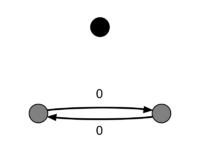
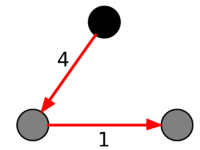
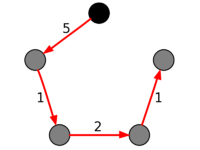
Пример
Корректность
Замечания:
- После перевзвешивания в каждую вершину кроме входит по крайней мере одно ребро нулевого веса.
- Пусть — искомое дерево в с весовой функцией . , т.е. - MST в с весовой функцией тогда и только тогда, когда — MST в с весовой функцией .
| Лемма: |
Кратчайшее дерево путей в графе можно получить, найдя кратчайшее дерево путей в графе , а затем заменив в нем каждую компоненту сильной связности деревом, построенным из дуг нулевой длинны. |
| Доказательство: |
| Зафиксируем любое дерево путей и покажем, что в графе найдется дерево не большей длины, имеющее такую структуру, как сказано в лемме. Для такой структуры дерева необходимо и достаточно, чтобы в каждое из подмножеств входило только по одному ребру. Меньше быть не может, иначе получится отдельная компонента связности. Если же в какое-то подмножество входит больше чем одно ребро, то все ребра кроме одного можно заменить ребрами нулевой длины, лежащими внутри подмножества, что разве лишь уменьшит длину дерева и не нарушит связности. Повторяя это преобразование нужное число раз мы добьемся искомой структуры дерева. |
Из сделанных замечаний и леммы следует, что дерево — MST в .
Реализация
Обозначения:
- Граф хранится в виде множества ребер + индекс корня.
- Множество ребер - список смежности.
- Ребро - структура {from, to, weight}.
- root - текущий корень.
Особенность реализации: алгоритму не важна кратность ребер, поэтому при составлении нового графа кратные ребра могут появиться - это уменьшает асимптотику с до
Проверяем, можно ли дойти из до остальных вершин. Если можно - запускаем findMST. int findMST(edges, n, root): int res = 0 int minEdge[n] // создаем массив минимумов, входящих в каждую компоненту, инициализируем бесконечностью. for each edges minEdge[e.to] = min(e.w, minEdge[e.to]) for each res += minEdge[v] //веса минимальных ребер точно будут в результате edge zeroEdges[] //создаем массив нулевых ребер for each edges if e.w == minEdge[e.to] zeroEdges.pushback() // - ребро е, уменьшенное на минимальный вес, входящий в e.to if dfs(root, zeroEdges) // проверяем, можно ли дойти до всех вершин по нулевым ребрам return res int newComponents[n] // будущие компоненты связности newComponents = Сondensation(zeroEdges) edge newEdges[] //создаем массив ребер в новом графе с вершинами в полученных компонентах for each edges if e.to и e.from в разных компонентах добавляем в newEdges ребро с концами в данных компонентах и весом e.w - minEdge[e.to] res += findMST(newEdges, ComponentsCount, newComponents[root]) return res
Сложность
Всего будет построено не более конденсаций. Конденсацию можно построить за . Значит, алгоритм можно реализовать за .
Источники
- Романовский И. В. Дискретный анализ, 3-е изд., перераб. и доп. - СПб.:Невский Диалект; БХВ-Петербург, 2003. - 320 с.: ил. - ISBN 5-7940-0114-3
- http://is.ifmo.ru