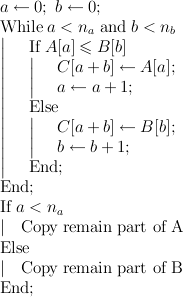Сортировка слиянием
Сортировка слиянием
Сортировка слиянием — вероятно, один из самых простых алгоритмов сортировки (среди «быстрых» алгоритмов).Сортировка слиянием — стабильный алгоритм сортировки. Это означает, что порядок «равных» элементов не изменяется в результате работы алгоритма. В некоторых задачах это свойство достаточно важно. Этот алгоритм был предложен Джоном фон Нейманом в 1945 году.
Принцип работы
Эта сортировка — хороший пример использования принципа «разделяй и властвуй». Сначала задача разбивается на несколько подзадач меньшего размера. Затем эти задачи решаются с помощью рекурсивного вызова или непосредственно, если их размер достаточно мал. Наконец, их решения комбинируются, и получается решение исходной задачи.
Для решения задачи сортировки эти три этапа выглядят так:
- Сортируемый массив разбивается на две части примерно одинакового размера;
- Каждая из получившихся частей сортируется отдельно, например — тем же самым алгоритмом;
- Два упорядоченных массива половинного размера соединяются в один.
Рекурсивное разбиение задачи на меньшие происходит до тех пор, пока размер массива не достигнет единицы (любой массив длины 1 можно считать упорядоченным).
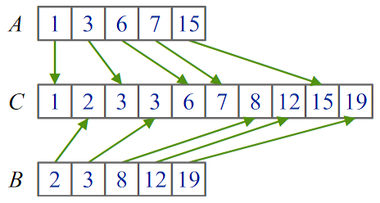
Слияние 2-х массивов
Допустим, у нас есть два отсортированных массива А и B размерами и соответственно, и мы хотим объединить их элементы в один большой отсортированный массив C размером . Для этого можно применить процедуру слияния, суть которой заключается в повторяющемся «отделении» элемента, наименьшего из двух имеющихся в началах исходных массивов, и присоединении этого элемента к концу результирующего массива. Элементы мы переносим до тех пор, пока один из исходных массивов не закончится. После этого оставшийся «хвост» одного из входных массивов дописывается в конец результирующего массива. Пример работы процедуры показан на рисунке:
Алгоритм слияния формально можно записать следующим образом:
