Деревья Эйлерова обхода
Введение
Динамические деревья (англ.dynamic tree) используются в двух областях:.........
Нужно поддерживать следующие операции
- — добавить ребро (u, w) (при условии, что вершины u w принадлежат разным деревьям)
- — разрезать ребро (u, w) (при условии, что ребро (u, w) принадлежит дереву),
- — принадлежат ли вершины u и w одной компоненте связности.
Euler tour tree - The data structure we'll develop can perform these operations time O(log n) each.
Euler Tours on Trees
Euler Tours
In a graph G, an Euler tour is a path through the graph that visits every edge exactly once.
Mathematically formulates the “trace this figure without picking up your pencil or redrawing any lines” puzzles.
Euler Tours on Trees
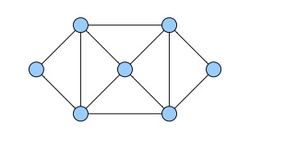
In general, trees do not have Euler tours.
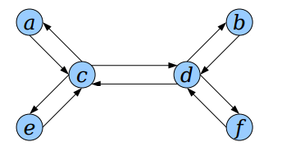
Technique: replace each edge {u, v} with two edges (u, v) and (v, u).
Resulting graph has an Euler tour.
High-level idea: Instead of storing the trees in the forest, store their Euler tours.
Each edge insertion or deletion translates into a set of manipulations on the Euler tours of the trees in the forest.
Checking whether two nodes are connected can be done by checking if they're in the same Euler tour.
Properties of Euler Tours
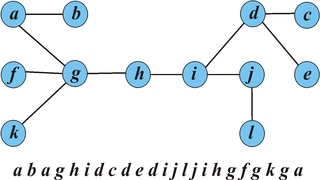
The sequence of nodes visited in an Euler tour of a tree is closely connected to the structure of the tree.
Begin by directing all edges toward the the first node in the tour.
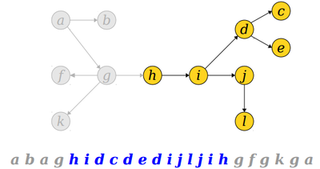
Claim: The sequences of nodes visited between the first and last instance of a node v gives an Euler tour of the subtree rooted at v.
Операции
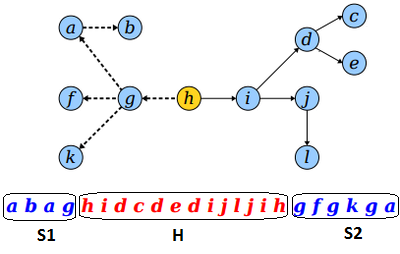
Rerooting a Tour
The subtrees defined by ranges in Euler tours on trees depend on the root.
In some cases, we will need to change the root of the tree.
Algorithm:
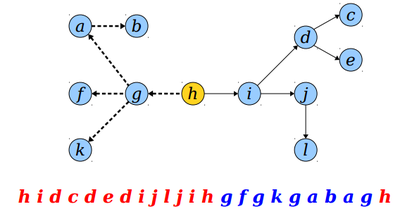
Split the tour into three parts: S₁, R, and S₂, where R consists of the nodes between the first and last occurrence of the new root r.
Delete the first node in S₁.
Concatenate R, S₂, S₁, {r}.
link(u ,v)
Given two trees T₁ and T₂, where u ∈ T₁ and v ∈ T₂, executing link(u, v) links the trees together by adding edge {u, v}.
Watch what happens to the Euler tours:
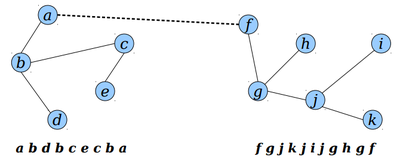
To link T₁ and T₂ by adding {u, v}:
Let E₁ and E₂ be Euler tours of T₁ and T₂, respectively.
Rotate E₁ to root the tour at u.
Rotate E₂ to root the tour at v.
Concatenate E₁, E₂, {u}.
cut(u ,v)
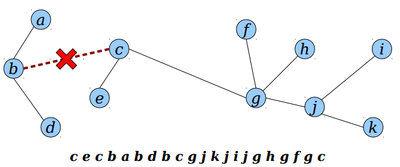
Given a tree T, executing cut(u, v) cuts the edge {u, v} from the tree (assuming it exists).
Watch what happens to the Euler tour of T:
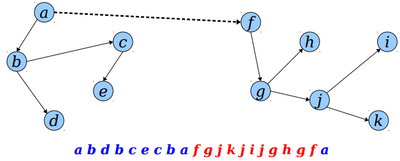
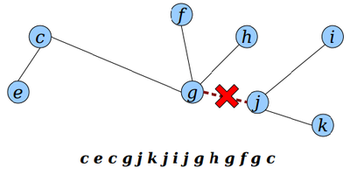
To cut T into T₁ and T₂ by cutting {u, v}:
Let E be an Euler tour for T.
Rotate u to the front of E.
Split E into E₁, V, E₂, where V is the span between the first and last occurrence of v.
T₁ has the Euler tour formed by concatenating E₁ and E₂, deleting the extra u at the join point.
T₂ has Euler tour V.
Реализация структуры
Goal: Implement link, cut, and is-connected as efficiently as possible.
By representing trees via their Euler tours, can implement link and cut so that only O(1) joins and splits are necessary per operation.
Questions to answer:
How do we efficiently implement these joins and splits?
Once we have the tours, how do we answer connectivity queries?
Implementing the Structure
The operations we have seen require us to be able to efficiently do the following:
Identify the first and last copy of a node in a sequence.
Split a sequence at those positions.
Concatenate sequences.
Add a new copy of a node to a sequence.
Delete a duplicate copy of a node from a sequence.
How do we do this efficiently?
Linked Lists
Balanced Trees
Сравнительная табличка
Похожие структуры
Про link-cut trees