Алгоритм Карккайнена-Сандерса
Алгоритм Карккайнена-Сандерса (Kärkkäinen, Sanders) — алгоритм построения суффиксного массива за линейное время.
Содержание
Используемые обозначения
- В данном конспекте используется 0-индексация.
- — подстрока строки с -го по -й символы включительно.
- Пусть длина строки равна . Обозначим , где как строку , дополненную защитными символами до длины .
Алгоритм «разделяй и властвуй»
| Определение: |
| Четным суффиксом назовем суффикс, начинающийся в четной позиции. Нечетным суффиксом — суффикс, начинающийся в нечетной позиции. |
- Строим суффиксный массив для нечетных суффиксов, рекурсивно сведя задачу к построению суффиксного массива для строки половинной длины.
- Строим суффиксный массив для четных суффиксов за линейное время, используя результат первого шага.
- Сливаем суффиксные массивы за линейное время.
Получили асимптотическое уравнение , решением которого является .
Для упрощения алгоритма вначале дополним нашу строку до четной длины (например, добавлением в конец). На шаге слияния мы сможем избавиться от него.
База рекурсии
Если длина текущей строки равна двум, надо выполнить обычное сравнение суффиксов.
Суффиксный массив для нечетных суффиксов
- Отобразим исходную строку длины в строку длины следующим образом:
- Сделаем список, состоящий из пар символов вида , где .
- Отсортируем его цифровой сортировкой за линейное время и получим новый алфавит .
- Перекодируем строку в алфавит , получив строку половинной длины.
- Рекурсивно построим суффиксный массив .
- Построим суффиксный массив . Очевидно, , так отношение упорядоченности любых двух строк в старом алфавите эквивалентно отношению упорядоченности в новом алфавите по его построению.
Суффиксный массив для четных суффиксов
На этом шаге мы за линейное время получим суффиксный массив для четных суффиксов, используя уже построенный .
Заметим, что сортировка множества четных суффиксов аналогична сортировке множества пар . Однако — нечетный суффикс, и его относительную позицию мы уже узнали на шаге 1.
Таким образом, чтобы отсортировать эти пары за линейное время, сначала сразу выпишем их в порядке возрастания второго элемента пары (то есть в порядке вхождения в массив ), а потом отсортируем устойчивой сортировкой подсчетом по первым элементам. После этого легко можно восстановить массив :
M = []
for i = 0 to n / 2 - 1
M.add(Pair(S[[i] - 1], [i]))
quick_stable_sort(M)
= []
for i = 0 to n/2 - 1:
.add(M[i].second - 1)
Заметим, что массив перед сортировкой подсчетом не был явно отсортирован по вторым элементам, и хранил не суффиксы, а их позиции в строке , но важно, что он был отсортирован по возрастанию соответствующих этим позициям нечетных суффиксов.
Получили, что весь второй шаг требует времени.
Слияние суффиксных массивов
Для суффиксного дерева третий шаг алгоритма опирается на специфические особенности суффиксных деревьев, которые не присущи суффиксным массивам[1] . В случае суффиксного массива слияние становится очень сложным, но все же оно было реализовано в алгоритме Ким-Сим-Парк-Парка[2]. Однако простой модификацией алгоритма можно значительно упростить его.
Пример
Покажем первые два шага агоритма для строки ababbbaa.
Во-первых, добавив защитный символ $, получив строку ababbbaa$ (для этого алгоритма он не требуется, но может понадобиться в применениях суффиксного массива). Во-вторых, дополним ее до четной длины, получив ababbbaa$$.
Суффиксный массив для нечетных суффиксов
- В новом алфавите будет четыре элемента — ba, bb, a$, $$. После сортировки они получат номера 2, 3, 1 и 0 соответственно.
- Переводим строку = babbbaa$$$ в новый алфавит. Сжатой строкой будет 23210.
- После рекурсивного вызова получим, что = [4, 3, 2, 0, 1], и = [9, 7, 5, 1, 3].
Суффиксный массив для четных суффиксов
- Обойдя массив , получим = [(, 9), (, 7), (, 5), (, 1), (, 3)].
- После сортировки подсчетом по первому элементу, получим = [(, 9), (, 7), (, 1), (, 3), (, 5)].
- Восстановив массив , получаем [8, 6, 0, 2, 4], что действительно является суффиксным массивом для четных суффиксов.
Слияние суффиксных массивов
Если бы мы умели сливать и за линейное время, получили бы:
| № | Подстрока |
|---|---|
Как и было сказано вначале, избавиться от лишних $ легко, так как суффиксы, им соответствующие, будут первыми в суффиксном массиве (в данном случае достаточно выбросить "9" из суффиксного массива).
Алгоритм Карккайнена-Сандерса
Изменим изначальный алгоритм следующим образом:
- Построим суффиксный массив для суффиксов, соответствующих позициям, не кратным трем. Рекурсивно сведем это к построению суффиксного массива для строки длиной в две трети исходной.
- Построим суффиксный массив для суффиксов, соответствующих кратным трем позициям, используя результат первого шага, за линейное время.
- Сольем эти суффиксные массивы в один за линейное время.
Получили асимптотическое уравнение , решением которого также является (это видно из того, что сумма геометрической прогрессии с основанием равна ).
Аналогично первой версии алгоритма, дополним строку до длины, кратной трем, защитными символами и получим .
- База рекурсии
Для этого алгоритма минимальной базой рекурсии будет строка длиной 4, так как она дополняется до длины 6, после чего вновь следует рекурсивный вызов строки длиной 4, и, если бы база была меньше 4, алгоритм вошел бы в бесконечную рекурсию. На этом этапе также можно применить обычную сортировку суффиксов, так как это потребует действий.
- Суффиксный массив для позиций не кратных 3
На этом шаге строится суффиксный массив для множества суффиксов .
- Получим строку аналогично предыдущему алгоритму:
- Сделаем список, состоящий из троек , где .
- Отсортируем его за линейное время цифровой сортировкой и получим новый алфавит .
- Перекодируем строку в строку длиной в алфавите . Тогда суффиксу в старом алфавите, где , в новом алфавите будет соответствовать строка , а если , то строка .
- Вызовем алгоритм рекурсивно для строки , получив суффиксный массив .
- Пройдем по массиву . Если , то этот суффикс соответствует позиции в строке , если же , то этот суффикс соответствует позиции в строке . Псевдокод получения :
= [] for i = 0 to .length - 1: if [i] < n/3: .add(3 * [i] + 1) else: .add(3 * ([i] - n/3) + 2)
- Суффиксный массив для позиций кратных 3
Этот шаг также аналогичен первой версии алгоритма. Сортировка множества аналогична сортировке пар , где — суффиксы в позициях, равных 1 по модулю 3, относительный порядок которых уже известен. Выпишем эти пары в порядке вхождения их в и отсортируем по первому элементу устойчивой сортировкой подсчетом, получив суффиксный массив . Псевдокод этого шага:
= [] M = [] for i = 0 to 2n/3 - 1: if [i] % 3 == 1: M.add(Pair(S*[[i] - 1], [i])) stable_sort(M) for i = 0 to n/3 - 1: .add(M[i].second - 1)
Аналогично, второй шаг требует времени.
- Слияние суффиксных массивов
На этом шаге мы должны слить суффиксные массивы и , чтобы получить суффиксный массив для всей строки .
Применим стандартный алгоритм слияния двух отсортированных массивов. Заметим, что явно массивы не отсортированы, но соответствующие элементам массива суффиксы — отсортированы.
Пусть на какой-то итерации слияния мы сравниваем суффиксы, соответствующие позициям , равной 1 по модулю 3, и (она всегда будет равна 0 по модулю 3). Это аналогично сравнению пар и . Сравнить первые элементы пар мы можем за , а относительный порядок вторых элементов пар нам уже известен, так как они соответствуют позициям, равным 2 и 1 по модулю 3 соответственно.
Аналогично, пусть на какой-то итерации слияния мы сравниваем суффиксы, соответствующие позициям , равной 2 по модулю 3, и (она всегда будет равна 0 по модулю 3). Тогда это аналогично сравнению троек и , что также можно делать за .
Псевдокод этой фазы:
= [] // Вначале предподсчитаем за O(n) обратную перестановку для суффиксного массива , то есть массив rank такой, что [rank[i]] = i. // Тогда мы сможем за O(1) сравнивать суффиксы по их позиции. rank = inverse() while i < 2 * n/3 and j < n/3: pos12 = [i] pos0 = [j] if pos12 % 3 == 1: if Pair(S*[pos12], rank[pos12 + 1]) < Pair(S*[pos0], rank[pos0 + 1]): .add(pos12) i++ else: .add(pos0) j++ else: if Triple(S*[pos12], S*[pos12 + 1], rank[pos12 + 2]) < Triple(S*[pos0], S*[pos0 + 1], rank[pos0 + 2]): .add(pos12) i++ else: .add(pos0) j++ while i < 2 * n/3: .add([i]) i++ while j < n/3: .add([j]) j++
Таким образом, получили простой метод слияния за .
Пример
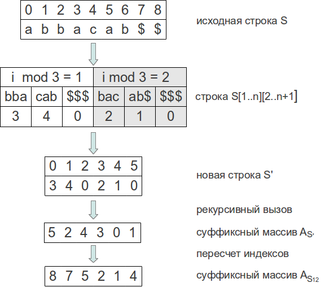
Построим суффиксный массив для строки abbacab. После добавления защитного символа и дополнения до кратной трем длины, получим abbacab$$.
- Суффиксный массив для позиций не кратных 3
- Тройками, соответствующими равными 1 по модулю 3 позициям, будут: bba, cab, $$$, соответствующими равным 2 по модулю 3 — bac, ab$, $$$. Новый алфавит будет содержать элементы bba, cab, $$$, bac, ab$, которые после сортировки получат номера 3, 4, 0, 2, 1 соответственно.
- Строкой bbacab$$$bacab$$$$ в новом алфавите будет = 340210.
- После рекурсивного вызова получим = [5, 2, 4, 3, 0, 1]. Пересчитав , получим [(5 - 3)*3 + 2, 2 * 3 + 1, (4 - 3) * 3 + 2, (3 - 3) * 3 + 2, 0 * 3 + 1, 1 * 3 + 1] = [8, 7, 5, 2, 1, 4].
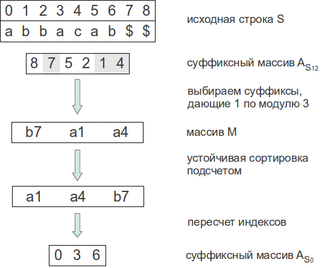
- Суффиксный массив для позиций кратных 3
- Обойдя массив и выбрав в нем элементы, равные 1 по модулю 3, получим массив пар = [(, 7), (, 1), (, 4)]
- После устойчивой сортировки подсчетом по первому элементу, получим = [(a, 1), (a, 4), (b, 7)]
- Восстановив , получаем [0, 3, 6].
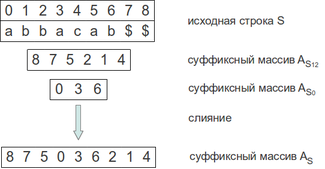
- Слияние суффиксных массивов
Рассмотрим, к примеру, третью итерацию слияния, к этой итерации массив = [8, 7], = 2, = 0, на ней мы сливаем суффиксы, соответствующие позициям 5 и 0.
- Образуем тройки и .
- После получения относительного порядка суффиксов, получим тройки (a, b, 1) и (a, b, 3). Первая тройка меньше второй, поэтому добавляем суффикс, соответствующий позиции 5 в массив .
- В конце итерации получаем = [8, 7, 5], = 3, = 0.
К концу слияния получим = [8, 7, 5, 0, 3, 6, 2, 1, 4]. Так как мы добавляли один символ в начале алгоритма для дополнения строки до длины, кратной трем, выбросим последний суффикс из , получим в итоге, что = [7, 5, 0, 3, 6, 2, 1, 4].
| № | Подстрока |
|---|---|
Заметим, что № 9 будет выброшен, так как в начале алгоритма был добавлен один к строке
Обобщение алгоритма
Массив LCP можно получить за линейное время алгоритмом Касаи.
На самом деле, алгоритм можно обобщить[3], взяв на первом шаге, к примеру, суффиксы, позиции которых по модулю 7 дают 3, 5 и 6. Для этого потребуются некоторое усложнение алгоритма, например, сортировка оставшихся суффиксов в нескольких группах на шаге 2 и слияние нескольких групп на шаге 3, но основная идея алгоритма остается той же. Множества, которые можно выбрать, на первом шаге определяются разностным покрытием (difference cover).
| Определение: |
| Разностное покрытие (англ. difference cover) по модулю — множество чисел от до таких, что . |
Например, является разностным покрытием по модулю , является разностным покрытием по модулю , а — не является разностным покрытием по модулю , поэтому этот алгоритм не применим к нему. Подробнее узнать, как вычислять разностное покрытие для заданного модуля можно также здесь[3].
См. также
Примечания
- ↑ M. Farach. Optimal suffix tree construction with large alphabets. http://www.cs.rutgers.edu/~farach/pubs/FarFerrMuthu00.pdf
- ↑ D. K. Kim, J. S. Sim, H. Park, and K. Park. Linear-time construction of suffix arrays. http://www.springerlink.com/content/568156021q45r320/
- ↑ 3,0 3,1 Juha Kärkkäinen, Peter Sanders and Stefan Burkhardt. Linear work suffix array construction. http://www.cs.helsinki.fi/juha.karkkainen/publications/jacm05-revised.pdf