Алгоритм Кока-Янгера-Касами разбора грамматики в НФХ — различия между версиями
Kabanov (обсуждение | вклад) (→Пример работы) |
Gaporf (обсуждение | вклад) м (→Контекстно-свободная грамматика: тире) |
||
| (не показано 15 промежуточных версий 3 участников) | |||
| Строка 3: | Строка 3: | ||
Пусть дана [[Контекстно-свободные грамматики, вывод, лево- и правосторонний вывод, дерево разбора|контекстно-свободная грамматика]] <tex>\Gamma</tex> в [[нормальная форма Хомского|нормальной форме Хомского]] и слово <tex>w \in \Sigma^{*}</tex>. Требуется выяснить, выводится ли это слово в данной грамматике. | Пусть дана [[Контекстно-свободные грамматики, вывод, лево- и правосторонний вывод, дерево разбора|контекстно-свободная грамматика]] <tex>\Gamma</tex> в [[нормальная форма Хомского|нормальной форме Хомского]] и слово <tex>w \in \Sigma^{*}</tex>. Требуется выяснить, выводится ли это слово в данной грамматике. | ||
}} | }} | ||
| + | |||
| + | == Контекстно-свободная грамматика == | ||
| + | {{Определение | ||
| + | |definition = | ||
| + | '''[[Контекстно-свободные грамматики, вывод, лево- и правосторонний вывод, дерево разбора|Контекстно-свободная грамматика]]''' ('''КС-грамматика''', '''бесконтекстная грамматика''') {{---}} способ описания формального языка, представляющий собой четверку | ||
| + | <tex>\Gamma =\langle \Sigma, N, S \in N, P \subset N^{+}\times (\Sigma\cup N)^{*}\rangle</tex>, где: | ||
| + | * <tex>\Sigma</tex> {{---}} [[Основные_определения: алфавит, слово, язык, конкатенация, свободный моноид слов|алфавит]], элементы которого называют '''терминалами''' (англ. ''terminals'') | ||
| + | * <tex>N</tex> {{---}} множество, элементы которого называют '''нетерминалами''' (англ. ''nonterminals'') | ||
| + | * <tex>S</tex> {{---}} начальный символ грамматики (англ. ''start symbol'') | ||
| + | * <tex>P</tex> {{---}} набор правил вывода (англ. ''production rules'' или ''productions'') вида <tex>A \rightarrow B_1 B_2 \ldots B_n</tex>, где <tex>A \in N</tex>, <tex>B_i \in \Sigma \cup N</tex>, то есть у которых левые части {{---}} одиночные нетерминалы, а правые {{---}} последовательности терминалов и нетерминалов. | ||
| + | }} | ||
| + | === Пример === | ||
| + | |||
| + | Терминалы <tex>\Sigma = \{(, )\}</tex>. | ||
| + | |||
| + | Нетерминалы <tex>N = \{S\}</tex>. | ||
| + | |||
| + | Правила вывода <tex>P</tex>: | ||
| + | |||
| + | <tex>\begin{array}{l l} | ||
| + | S \rightarrow \varepsilon\\ | ||
| + | S \rightarrow SS\\ | ||
| + | S \rightarrow (S)\\ | ||
| + | \end{array}</tex> | ||
| + | |||
| + | Данная грамматика задает язык [[Правильные_скобочные_последовательности|правильных скобочных последовательностей]]. Например, последовательность <tex>(()(()))</tex> может быть выведена следующим образом: | ||
| + | |||
| + | <tex> S \Rightarrow (S) \Rightarrow (SS) \Rightarrow (()(S)) \Rightarrow (()(())) </tex> | ||
| + | |||
| + | == Нормальная форма Хомского == | ||
| + | |||
| + | '''[[Нормальная форма Хомского]]''' {{---}} нормальная форма КС-грамматик, в которой все продукции имеют вид: | ||
| + | * <tex>A \rightarrow a</tex>, где <tex>A</tex> {{---}} нетерминал, а <tex>a</tex> {{---}} терминал | ||
| + | * <tex>A \rightarrow BC</tex>, где <tex>A</tex>, <tex>B</tex>, <tex>C</tex> {{---}} нетерминалы, причем <tex>B</tex> и <tex>C</tex> не являются начальными нетерминалами | ||
| + | * <tex>S \rightarrow \varepsilon</tex>, где <tex>S</tex> {{---}} начальный нетерминал и <tex>\varepsilon</tex> {{---}} пустая строка (данная продукция необходима, если в языке присуствует пустая строка) | ||
| + | |||
| + | [[Нормальная форма Хомского|Можно показать]], что любую КС-грамматику можно привести к нормальной форме Хомского. | ||
== Алгоритм == | == Алгоритм == | ||
| − | '''Алгоритм Кока-Янгера-Касами''' (англ. ''Cocke-Younger-Kasami algorithm'', англ. ''CYK - алгоритм'') {{---}} | + | '''Алгоритм Кока-Янгера-Касами''' (англ. ''Cocke-Younger-Kasami algorithm'', англ. ''CYK-алгоритм'') {{---}} алгоритм, позволяющий по слову узнать, выводимо ли оно в заданной КС-грамматике в нормальной форме Хомского. Любую КС-грамматику можно привести к НФХ, поэтому алгоритм является универсальным для любой КС-грамматики. |
| − | Будем решать задачу [[Динамическое_программирование|динамическим программированием]]. Дана строка <tex>w</tex> размером <tex>n</tex>. Заведем для неё трехмерный массив <tex>d</tex> размером <tex>| | + | |
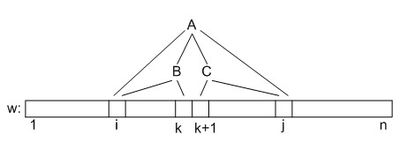
| + | Будем решать задачу [[Динамическое_программирование|динамическим программированием]]. Дана строка <tex>w</tex> размером <tex>n</tex>. Заведем для неё трехмерный массив <tex>d</tex> размером <tex>|N| \times n \times n</tex>, состоящий из логических значений, и <tex>d[A][i][j] = true \ </tex> тогда и только тогда, когда из нетерминала <tex>A</tex> правилами грамматики можно вывести подстроку <tex>w[i \ldots j]</tex>. | ||
Рассмотрим все пары <tex>\lbrace \langle j, i \rangle | j-i=m \rbrace</tex>, где <tex>m</tex> {{---}} константа и <tex>m < n</tex>. | Рассмотрим все пары <tex>\lbrace \langle j, i \rangle | j-i=m \rbrace</tex>, где <tex>m</tex> {{---}} константа и <tex>m < n</tex>. | ||
| − | * <tex>i = j</tex>. Инициализируем массив для всех нетерминалов, из которых выводится какой-либо символ строки <tex>w</tex>. В таком случае <tex>d[A][i][i] = true</tex>, если в грамматике <tex>\Gamma</tex> присутствует правило <tex>A \rightarrow w[i]</tex>. Иначе <tex>d[A][i][i] = false</tex>. | + | * <tex>i = j</tex>. Инициализируем массив для всех нетерминалов, из которых выводится какой-либо символ строки <tex>w</tex>. В таком случае <tex>d[A][i][i] = true \ </tex>, если в грамматике <tex>\Gamma</tex> присутствует правило <tex>A \rightarrow w[i]</tex>. Иначе <tex>d[A][i][i] = false</tex>. |
| − | * <tex>i \ne j</tex>. Значения для всех нетерминалов и пар <tex>\lbrace \langle j', i' \rangle | j' - i' < m \rbrace</tex> уже вычислены, поэтому <tex>d[A][i][j] = \bigvee\limits_{A \rightarrow BC}\bigvee\limits_{k = i}^{j-1} d[B][i][k] \wedge d[C][k+1][j]</tex>. То есть, подстроку <tex>w[i \ | + | * <tex>i \ne j</tex>. Значения для всех нетерминалов и пар <tex>\lbrace \langle j', i' \rangle | j' - i' < m \rbrace</tex> уже вычислены, поэтому <tex>d[A][i][j] = \bigvee\limits_{A \rightarrow BC}\bigvee\limits_{k = i}^{j-1} d[B][i][k] \wedge d[C][k+1][j] \ \ </tex>. То есть, подстроку <tex>w[i \ldots j]</tex> можно вывести из нетерминала <tex>A</tex>, если существует продукция вида <tex>A \rightarrow BC</tex> и такое <tex>k</tex>, что подстрока <tex>w[i \ldots k]</tex> выводима из <tex>B</tex>, а подстрока <tex>w[k + 1 \ldots j]</tex> выводится из <tex>C</tex>. |
[[Файл:CYK_rule_2.jpg|400px]] | [[Файл:CYK_rule_2.jpg|400px]] | ||
| Строка 20: | Строка 58: | ||
=== Количество способов вывести слово === | === Количество способов вывести слово === | ||
| − | Если массив будет хранить целые числа, а формулу заменить на <tex>d[A][i][j] = \sum\limits_{A \rightarrow BC}\sum\limits_{k = i}^{j-1} d[B][i][k] \cdot d[C][k + 1][j]</tex>, то <tex>d[A][i][j]</tex> {{---}} количество способов получить подстроку <tex>w[i \ | + | Если массив будет хранить целые числа, а формулу заменить на <tex>d[A][i][j] = \sum\limits_{A \rightarrow BC}\sum\limits_{k = i}^{j-1} d[B][i][k] \cdot d[C][k + 1][j] \ \ </tex>, то <tex>d[A][i][j]</tex> {{---}} количество способов получить подстроку <tex>w[i \ldots j]</tex> из нетерминала <tex>A</tex>. |
=== Минимальная стоимость вывода слова === | === Минимальная стоимость вывода слова === | ||
| − | Пусть <tex> | + | Пусть <tex>H(A \rightarrow BC)</tex> {{---}} стоимость вывода по правилу <tex>A \rightarrow BC</tex>. Тогда, если использовать формулу <tex>d[A][i][j] = \min\limits_{A \rightarrow BC} \min\limits_{k = i}^{j-1} ( d[B][i][k] + d[C][k + 1][j] + H(A \rightarrow BC) ) \ \ </tex>, то <tex>d[A][i][j]</tex> {{---}} минимальная стоимость вывода подстроки <tex>w[i \ldots j]</tex> из нетерминала <tex>A</tex>. |
| − | Таким образом, задача о выводе в КС-грамматике в нормальной форме Хомского является | + | Таким образом, задача о выводе в КС-грамматике в нормальной форме Хомского является частным случаем задачи динамического программирования на подотрезке. |
== Асимптотика == | == Асимптотика == | ||
| − | Обработка правил вида <tex>A \rightarrow w[i]</tex> | + | Обработка правил вида <tex>A \rightarrow w[i]</tex> выполняется за <tex>O(n \cdot |\Gamma|)</tex>. |
| − | Проход по всем подстрокам | + | Проход по всем подстрокам выполняется за <tex>O(n^2)</tex>. В обработке одной подстроки присутствует цикл по всем правилам вывода и по всем разбиениям на две подстроки, следовательно обработка работает за <tex>O(n \cdot |\Gamma|)</tex>. В итоге получаем конечную сложность <tex>O(n^3 \cdot |\Gamma|)</tex>. |
| − | Следовательно, общее время работы алгоритма {{---}} <tex>O(n^3 \cdot |\Gamma|)</tex>. Кроме того, алгоритму требуется память | + | Следовательно, общее время работы алгоритма {{---}} <tex>O(n^3 \cdot |\Gamma|)</tex>. Кроме того, алгоритму требуется память на массив <tex>d</tex> объемом <tex>O(n^2 \cdot |N|)</tex>, где <tex>|N|</tex> {{---}} количество [[Формальные_грамматики#Определения|нетерминалов]] грамматики. |
== Пример работы == | == Пример работы == | ||
| − | Дана грамматика [[Правильные_скобочные_последовательности|правильных скобочных последовательностей]] <tex>\Gamma</tex> | + | Дана грамматика [[Правильные_скобочные_последовательности|правильных скобочных последовательностей]] <tex>\Gamma</tex> в нормальной форме Хомского. |
<tex>\begin{array}{l l} | <tex>\begin{array}{l l} | ||
| − | + | A \rightarrow \varepsilon\ |\ BB\ |\ CD\\ | |
| − | + | B \rightarrow BB\ |\ CD\\ | |
| − | + | C \rightarrow (\\ | |
| − | + | D \rightarrow BE\ |\ )\\ | |
| − | + | E \rightarrow )\\ | |
\end{array}</tex> | \end{array}</tex> | ||
| − | Дано слово <tex>w = | + | Дано слово <tex>w = ()(())</tex>. |
| − | |||
Инициализация массива <tex>d</tex>. | Инициализация массива <tex>d</tex>. | ||
| − | |||
{| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | {| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | ||
| − | ! colspan="7"|A | + | ! colspan="7" style="background:#ffdead;"|A |
|- | |- | ||
! | ! | ||
| Строка 70: | Строка 106: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 2 | ! 2 | ||
| Строка 79: | Строка 114: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 3 | ! 3 | ||
| Строка 88: | Строка 122: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 4 | ! 4 | ||
| Строка 97: | Строка 130: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 5 | ! 5 | ||
| Строка 106: | Строка 138: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 6 | ! 6 | ||
| Строка 115: | Строка 146: | ||
| | | | ||
| | | | ||
| − | |||
|} | |} | ||
{| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | {| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | ||
| − | ! colspan="7"|B | + | ! colspan="7" style="background:#ffdead;"|B |
|- | |- | ||
! | ! | ||
| Строка 129: | Строка 159: | ||
|- | |- | ||
! 1 | ! 1 | ||
| − | |||
| | | | ||
| | | | ||
| Строка 135: | Строка 164: | ||
| | | | ||
| | | | ||
| − | + | | | |
|- | |- | ||
! 2 | ! 2 | ||
| Строка 144: | Строка 173: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 3 | ! 3 | ||
| | | | ||
| | | | ||
| − | |||
| | | | ||
| | | | ||
| | | | ||
| − | + | | | |
|- | |- | ||
! 4 | ! 4 | ||
| Строка 159: | Строка 186: | ||
| | | | ||
| | | | ||
| − | |||
| | | | ||
| | | | ||
| − | + | | | |
|- | |- | ||
! 5 | ! 5 | ||
| Строка 171: | Строка 197: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 6 | ! 6 | ||
| Строка 180: | Строка 205: | ||
| | | | ||
| | | | ||
| − | |||
|} | |} | ||
{| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | {| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | ||
| − | ! colspan="7"|C | + | ! colspan="7" style="background:#ffdead;"|C |
|- | |- | ||
! | ! | ||
| Строка 194: | Строка 218: | ||
|- | |- | ||
! 1 | ! 1 | ||
| + | | align="center"| ● | ||
| | | | ||
| | | | ||
| Строка 199: | Строка 224: | ||
| | | | ||
| | | | ||
| − | |||
| − | |||
|- | |- | ||
! 2 | ! 2 | ||
| | | | ||
| − | |||
| | | | ||
| | | | ||
| | | | ||
| | | | ||
| − | + | | | |
|- | |- | ||
! 3 | ! 3 | ||
| | | | ||
| | | | ||
| + | | align="center"| ● | ||
| | | | ||
| | | | ||
| | | | ||
| − | |||
| − | |||
|- | |- | ||
! 4 | ! 4 | ||
| Строка 224: | Строка 245: | ||
| | | | ||
| | | | ||
| + | | align="center"| ● | ||
| | | | ||
| | | | ||
| − | |||
| − | |||
|- | |- | ||
! 5 | ! 5 | ||
| Строка 234: | Строка 254: | ||
| | | | ||
| | | | ||
| − | |||
| | | | ||
| − | + | | | |
|- | |- | ||
! 6 | ! 6 | ||
| Строка 244: | Строка 263: | ||
| | | | ||
| | | | ||
| − | | | + | | |
| − | |||
|} | |} | ||
{| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | {| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | ||
| − | ! colspan="7"|D | + | ! colspan="7" style="background:#ffdead;"|D |
|- | |- | ||
! | ! | ||
| Строка 265: | Строка 283: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 2 | ! 2 | ||
| | | | ||
| + | | align="center"| ● | ||
| | | | ||
| | | | ||
| | | | ||
| | | | ||
| − | |||
| − | |||
|- | |- | ||
! 3 | ! 3 | ||
| Строка 283: | Строка 299: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 4 | ! 4 | ||
| Строка 292: | Строка 307: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 5 | ! 5 | ||
| Строка 299: | Строка 313: | ||
| | | | ||
| | | | ||
| + | | align="center"| ● | ||
| | | | ||
| − | |||
| − | |||
|- | |- | ||
! 6 | ! 6 | ||
| Строка 309: | Строка 322: | ||
| | | | ||
| | | | ||
| − | | | + | | align="center"| ● |
| − | |||
|} | |} | ||
| − | {| border="1" class="wikitable" style="width: 150px; height: 150px; " | + | {| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" |
| − | ! colspan="7"|E | + | ! colspan="7" style="background:#ffdead;"|E |
|- | |- | ||
! | ! | ||
| Строка 330: | Строка 342: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 2 | ! 2 | ||
| Строка 339: | Строка 350: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 3 | ! 3 | ||
| Строка 348: | Строка 358: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 4 | ! 4 | ||
| Строка 357: | Строка 366: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 5 | ! 5 | ||
| Строка 366: | Строка 374: | ||
| align="center"| ● | | align="center"| ● | ||
| | | | ||
| − | |||
|- | |- | ||
! 6 | ! 6 | ||
| Строка 375: | Строка 382: | ||
| | | | ||
| align="center"| ● | | align="center"| ● | ||
| − | |||
|} | |} | ||
| − | + | <div style="clear:both;"></div> | |
| − | |||
Заполнение массива <tex>d</tex>. | Заполнение массива <tex>d</tex>. | ||
| − | |||
| − | |||
| − | |||
| + | Итерация <tex>m = 1</tex>. | ||
{| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | {| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | ||
| − | ! colspan="7"|A | + | ! colspan="7" style="background:#ffdead;"|A |
|- | |- | ||
! | ! | ||
| Строка 405: | Строка 408: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 2 | ! 2 | ||
| Строка 414: | Строка 416: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 3 | ! 3 | ||
| Строка 423: | Строка 424: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 4 | ! 4 | ||
| Строка 432: | Строка 432: | ||
| align="center"| ● | | align="center"| ● | ||
| | | | ||
| − | |||
|- | |- | ||
! 5 | ! 5 | ||
| Строка 441: | Строка 440: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 6 | ! 6 | ||
| Строка 450: | Строка 448: | ||
| | | | ||
| | | | ||
| − | |||
|} | |} | ||
{| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | {| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | ||
| − | ! colspan="7"|B | + | ! colspan="7" style="background:#ffdead;"|B |
|- | |- | ||
! | ! | ||
| Строка 464: | Строка 461: | ||
|- | |- | ||
! 1 | ! 1 | ||
| + | | | ||
| align="center"| ● | | align="center"| ● | ||
| | | | ||
| Строка 469: | Строка 467: | ||
| | | | ||
| | | | ||
| − | |||
| − | |||
|- | |- | ||
! 2 | ! 2 | ||
| Строка 479: | Строка 475: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 3 | ! 3 | ||
| | | | ||
| | | | ||
| − | |||
| | | | ||
| | | | ||
| | | | ||
| − | + | | | |
|- | |- | ||
! 4 | ! 4 | ||
| + | | | ||
| | | | ||
| | | | ||
| Строка 496: | Строка 491: | ||
| align="center"| ● | | align="center"| ● | ||
| | | | ||
| − | |||
| − | |||
|- | |- | ||
! 5 | ! 5 | ||
| Строка 506: | Строка 499: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 6 | ! 6 | ||
| Строка 515: | Строка 507: | ||
| | | | ||
| | | | ||
| − | |||
|} | |} | ||
{| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | {| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | ||
| − | ! colspan="7"|C | + | ! colspan="7" style="background:#ffdead;"|C |
|- | |- | ||
! | ! | ||
| Строка 529: | Строка 520: | ||
|- | |- | ||
! 1 | ! 1 | ||
| + | | align="center"| ● | ||
| | | | ||
| | | | ||
| Строка 534: | Строка 526: | ||
| | | | ||
| | | | ||
| − | |||
| − | |||
|- | |- | ||
! 2 | ! 2 | ||
| | | | ||
| − | |||
| | | | ||
| | | | ||
| | | | ||
| | | | ||
| − | + | | | |
|- | |- | ||
! 3 | ! 3 | ||
| | | | ||
| | | | ||
| + | | align="center"| ● | ||
| | | | ||
| | | | ||
| | | | ||
| − | |||
| − | |||
|- | |- | ||
! 4 | ! 4 | ||
| Строка 559: | Строка 547: | ||
| | | | ||
| | | | ||
| + | | align="center"| ● | ||
| | | | ||
| | | | ||
| − | |||
| − | |||
|- | |- | ||
! 5 | ! 5 | ||
| Строка 569: | Строка 556: | ||
| | | | ||
| | | | ||
| − | |||
| | | | ||
| − | + | | | |
|- | |- | ||
! 6 | ! 6 | ||
| Строка 579: | Строка 565: | ||
| | | | ||
| | | | ||
| − | | | + | | |
| − | |||
|} | |} | ||
{| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | {| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | ||
| − | ! colspan="7"|D | + | ! colspan="7" style="background:#ffdead;"|D |
|- | |- | ||
! | ! | ||
| Строка 595: | Строка 580: | ||
! 1 | ! 1 | ||
| | | | ||
| − | |||
| | | | ||
| | | | ||
| | | | ||
| | | | ||
| − | + | | | |
|- | |- | ||
! 2 | ! 2 | ||
| | | | ||
| + | | align="center"| ● | ||
| | | | ||
| | | | ||
| | | | ||
| | | | ||
| − | |||
| − | |||
|- | |- | ||
! 3 | ! 3 | ||
| Строка 618: | Строка 601: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 4 | ! 4 | ||
| Строка 625: | Строка 607: | ||
| | | | ||
| | | | ||
| − | |||
| | | | ||
| − | + | | | |
|- | |- | ||
! 5 | ! 5 | ||
| Строка 634: | Строка 615: | ||
| | | | ||
| | | | ||
| + | | align="center"| ● | ||
| | | | ||
| − | |||
| − | |||
|- | |- | ||
! 6 | ! 6 | ||
| Строка 644: | Строка 624: | ||
| | | | ||
| | | | ||
| − | | | + | | align="center"| ● |
| − | |||
|} | |} | ||
| − | {| border="1" class="wikitable" style="width: 150px; height: 150px; " | + | {| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" |
| − | ! colspan="7"|E | + | ! colspan="7" style="background:#ffdead;"|E |
|- | |- | ||
! | ! | ||
| Строка 665: | Строка 644: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 2 | ! 2 | ||
| Строка 674: | Строка 652: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 3 | ! 3 | ||
| Строка 683: | Строка 660: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 4 | ! 4 | ||
| Строка 692: | Строка 668: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 5 | ! 5 | ||
| Строка 701: | Строка 676: | ||
| align="center"| ● | | align="center"| ● | ||
| | | | ||
| − | |||
|- | |- | ||
! 6 | ! 6 | ||
| Строка 710: | Строка 684: | ||
| | | | ||
| align="center"| ● | | align="center"| ● | ||
| − | |||
|} | |} | ||
| − | + | <div style="clear:both;"></div> | |
| − | |||
| − | |||
| + | Итерация <tex>m = 2</tex>. | ||
{| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | {| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | ||
| − | ! colspan="7"|A | + | ! colspan="7" style="background:#ffdead;"|A |
|- | |- | ||
! | ! | ||
| Строка 735: | Строка 707: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 2 | ! 2 | ||
| Строка 744: | Строка 715: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 3 | ! 3 | ||
| Строка 753: | Строка 723: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 4 | ! 4 | ||
| Строка 762: | Строка 731: | ||
| align="center"| ● | | align="center"| ● | ||
| | | | ||
| − | |||
|- | |- | ||
! 5 | ! 5 | ||
| Строка 771: | Строка 739: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 6 | ! 6 | ||
| Строка 780: | Строка 747: | ||
| | | | ||
| | | | ||
| − | |||
|} | |} | ||
{| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | {| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | ||
| − | ! colspan="7"|B | + | ! colspan="7" style="background:#ffdead;"|B |
|- | |- | ||
! | ! | ||
| Строка 794: | Строка 760: | ||
|- | |- | ||
! 1 | ! 1 | ||
| + | | | ||
| align="center"| ● | | align="center"| ● | ||
| | | | ||
| Строка 799: | Строка 766: | ||
| | | | ||
| | | | ||
| − | |||
| − | |||
|- | |- | ||
! 2 | ! 2 | ||
| Строка 809: | Строка 774: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 3 | ! 3 | ||
| | | | ||
| | | | ||
| − | |||
| | | | ||
| | | | ||
| | | | ||
| − | + | | | |
|- | |- | ||
! 4 | ! 4 | ||
| + | | | ||
| | | | ||
| | | | ||
| Строка 826: | Строка 790: | ||
| align="center"| ● | | align="center"| ● | ||
| | | | ||
| − | |||
| − | |||
|- | |- | ||
! 5 | ! 5 | ||
| Строка 836: | Строка 798: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 6 | ! 6 | ||
| Строка 845: | Строка 806: | ||
| | | | ||
| | | | ||
| − | |||
|} | |} | ||
{| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | {| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | ||
| − | ! colspan="7"|C | + | ! colspan="7" style="background:#ffdead;"|C |
|- | |- | ||
! | ! | ||
| Строка 859: | Строка 819: | ||
|- | |- | ||
! 1 | ! 1 | ||
| + | | align="center"| ● | ||
| | | | ||
| | | | ||
| Строка 864: | Строка 825: | ||
| | | | ||
| | | | ||
| − | |||
| − | |||
|- | |- | ||
! 2 | ! 2 | ||
| | | | ||
| − | |||
| | | | ||
| | | | ||
| | | | ||
| | | | ||
| − | + | | | |
|- | |- | ||
! 3 | ! 3 | ||
| | | | ||
| | | | ||
| + | | align="center"| ● | ||
| | | | ||
| | | | ||
| | | | ||
| − | |||
| − | |||
|- | |- | ||
! 4 | ! 4 | ||
| Строка 889: | Строка 846: | ||
| | | | ||
| | | | ||
| + | | align="center"| ● | ||
| | | | ||
| | | | ||
| − | |||
| − | |||
|- | |- | ||
! 5 | ! 5 | ||
| Строка 899: | Строка 855: | ||
| | | | ||
| | | | ||
| − | |||
| | | | ||
| − | + | | | |
|- | |- | ||
! 6 | ! 6 | ||
| Строка 909: | Строка 864: | ||
| | | | ||
| | | | ||
| − | | | + | | |
| − | |||
|} | |} | ||
{| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | {| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | ||
| − | ! colspan="7"|D | + | ! colspan="7" style="background:#ffdead;"|D |
|- | |- | ||
! | ! | ||
| Строка 925: | Строка 879: | ||
! 1 | ! 1 | ||
| | | | ||
| − | |||
| | | | ||
| | | | ||
| | | | ||
| | | | ||
| − | + | | | |
|- | |- | ||
! 2 | ! 2 | ||
| | | | ||
| + | | align="center"| ● | ||
| | | | ||
| | | | ||
| | | | ||
| | | | ||
| − | |||
| − | |||
|- | |- | ||
! 3 | ! 3 | ||
| Строка 948: | Строка 900: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 4 | ! 4 | ||
| + | | | ||
| | | | ||
| | | | ||
| Строка 956: | Строка 908: | ||
| | | | ||
| align="center"| ● | | align="center"| ● | ||
| − | |||
| − | |||
|- | |- | ||
! 5 | ! 5 | ||
| Строка 964: | Строка 914: | ||
| | | | ||
| | | | ||
| + | | align="center"| ● | ||
| | | | ||
| − | |||
| − | |||
|- | |- | ||
! 6 | ! 6 | ||
| Строка 974: | Строка 923: | ||
| | | | ||
| | | | ||
| − | | | + | | align="center"| ● |
| − | |||
|} | |} | ||
| − | {| border="1" class="wikitable" style="width: 150px; height: 150px; " | + | {| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" |
| − | ! colspan="7"|E | + | ! colspan="7" style="background:#ffdead;"|E |
|- | |- | ||
! | ! | ||
| Строка 995: | Строка 943: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 2 | ! 2 | ||
| Строка 1004: | Строка 951: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 3 | ! 3 | ||
| Строка 1013: | Строка 959: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 4 | ! 4 | ||
| Строка 1022: | Строка 967: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 5 | ! 5 | ||
| Строка 1031: | Строка 975: | ||
| align="center"| ● | | align="center"| ● | ||
| | | | ||
| − | |||
|- | |- | ||
! 6 | ! 6 | ||
| Строка 1040: | Строка 983: | ||
| | | | ||
| align="center"| ● | | align="center"| ● | ||
| − | |||
|} | |} | ||
| − | + | <div style="clear:both;"></div> | |
| − | |||
| − | |||
| + | Итерация <tex>m = 3</tex>. | ||
{| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | {| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | ||
| − | ! colspan="7"|A | + | ! colspan="7" style="background:#ffdead;"|A |
|- | |- | ||
! | ! | ||
| Строка 1065: | Строка 1006: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 2 | ! 2 | ||
| Строка 1074: | Строка 1014: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 3 | ! 3 | ||
| Строка 1083: | Строка 1022: | ||
| | | | ||
| align="center"| ● | | align="center"| ● | ||
| − | |||
|- | |- | ||
! 4 | ! 4 | ||
| Строка 1092: | Строка 1030: | ||
| align="center"| ● | | align="center"| ● | ||
| | | | ||
| − | |||
|- | |- | ||
! 5 | ! 5 | ||
| Строка 1101: | Строка 1038: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 6 | ! 6 | ||
| Строка 1110: | Строка 1046: | ||
| | | | ||
| | | | ||
| − | |||
|} | |} | ||
{| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | {| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | ||
| − | ! colspan="7"|B | + | ! colspan="7" style="background:#ffdead;"|B |
|- | |- | ||
! | ! | ||
| Строка 1124: | Строка 1059: | ||
|- | |- | ||
! 1 | ! 1 | ||
| + | | | ||
| align="center"| ● | | align="center"| ● | ||
| | | | ||
| Строка 1129: | Строка 1065: | ||
| | | | ||
| | | | ||
| − | |||
| − | |||
|- | |- | ||
! 2 | ! 2 | ||
| Строка 1139: | Строка 1073: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 3 | ! 3 | ||
| | | | ||
| | | | ||
| − | |||
| | | | ||
| | | | ||
| | | | ||
| − | + | | align="center"| ● | |
|- | |- | ||
! 4 | ! 4 | ||
| + | | | ||
| | | | ||
| | | | ||
| Строка 1156: | Строка 1089: | ||
| align="center"| ● | | align="center"| ● | ||
| | | | ||
| − | |||
| − | |||
|- | |- | ||
! 5 | ! 5 | ||
| Строка 1166: | Строка 1097: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 6 | ! 6 | ||
| Строка 1175: | Строка 1105: | ||
| | | | ||
| | | | ||
| − | |||
|} | |} | ||
{| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | {| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | ||
| − | ! colspan="7"|C | + | ! colspan="7" style="background:#ffdead;"|C |
|- | |- | ||
! | ! | ||
| Строка 1189: | Строка 1118: | ||
|- | |- | ||
! 1 | ! 1 | ||
| + | | align="center"| ● | ||
| | | | ||
| | | | ||
| Строка 1194: | Строка 1124: | ||
| | | | ||
| | | | ||
| − | |||
| − | |||
|- | |- | ||
! 2 | ! 2 | ||
| | | | ||
| − | |||
| | | | ||
| | | | ||
| | | | ||
| | | | ||
| − | + | | | |
|- | |- | ||
! 3 | ! 3 | ||
| | | | ||
| | | | ||
| + | | align="center"| ● | ||
| | | | ||
| | | | ||
| | | | ||
| − | |||
| − | |||
|- | |- | ||
! 4 | ! 4 | ||
| Строка 1219: | Строка 1145: | ||
| | | | ||
| | | | ||
| + | | align="center"| ● | ||
| | | | ||
| | | | ||
| − | |||
| − | |||
|- | |- | ||
! 5 | ! 5 | ||
| Строка 1229: | Строка 1154: | ||
| | | | ||
| | | | ||
| − | |||
| | | | ||
| − | + | | | |
|- | |- | ||
! 6 | ! 6 | ||
| Строка 1239: | Строка 1163: | ||
| | | | ||
| | | | ||
| − | | | + | | |
| − | |||
|} | |} | ||
{| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | {| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | ||
| − | ! colspan="7"|D | + | ! colspan="7" style="background:#ffdead;"|D |
|- | |- | ||
! | ! | ||
| Строка 1255: | Строка 1178: | ||
! 1 | ! 1 | ||
| | | | ||
| − | |||
| | | | ||
| | | | ||
| | | | ||
| | | | ||
| − | + | | | |
|- | |- | ||
! 2 | ! 2 | ||
| | | | ||
| + | | align="center"| ● | ||
| | | | ||
| | | | ||
| | | | ||
| | | | ||
| − | |||
| − | |||
|- | |- | ||
! 3 | ! 3 | ||
| Строка 1277: | Строка 1198: | ||
| | | | ||
| | | | ||
| − | | | + | | |
| − | |||
|- | |- | ||
! 4 | ! 4 | ||
| + | | | ||
| | | | ||
| | | | ||
| Строка 1286: | Строка 1207: | ||
| | | | ||
| align="center"| ● | | align="center"| ● | ||
| − | |||
| − | |||
|- | |- | ||
! 5 | ! 5 | ||
| Строка 1294: | Строка 1213: | ||
| | | | ||
| | | | ||
| + | | align="center"| ● | ||
| | | | ||
| − | |||
| − | |||
|- | |- | ||
! 6 | ! 6 | ||
| Строка 1304: | Строка 1222: | ||
| | | | ||
| | | | ||
| − | | | + | | align="center"| ● |
| − | |||
|} | |} | ||
| − | {| border="1" class="wikitable" style="width: 150px; height: 150px; " | + | {| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" |
| − | ! colspan="7"|E | + | ! colspan="7" style="background:#ffdead;"|E |
|- | |- | ||
! | ! | ||
| Строка 1325: | Строка 1242: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 2 | ! 2 | ||
| Строка 1334: | Строка 1250: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 3 | ! 3 | ||
| Строка 1343: | Строка 1258: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 4 | ! 4 | ||
| Строка 1352: | Строка 1266: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 5 | ! 5 | ||
| Строка 1361: | Строка 1274: | ||
| align="center"| ● | | align="center"| ● | ||
| | | | ||
| − | |||
|- | |- | ||
! 6 | ! 6 | ||
| Строка 1370: | Строка 1282: | ||
| | | | ||
| align="center"| ● | | align="center"| ● | ||
| − | |||
|} | |} | ||
| − | + | <div style="clear:both;"></div> | |
| − | |||
| − | |||
| + | Итерация <tex>m = 4</tex>. | ||
{| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | {| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | ||
| − | ! colspan="7"|A | + | ! colspan="7" style="background:#ffdead;"|A |
|- | |- | ||
! | ! | ||
| Строка 1395: | Строка 1305: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 2 | ! 2 | ||
| Строка 1404: | Строка 1313: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 3 | ! 3 | ||
| Строка 1413: | Строка 1321: | ||
| | | | ||
| align="center"| ● | | align="center"| ● | ||
| − | |||
|- | |- | ||
! 4 | ! 4 | ||
| Строка 1422: | Строка 1329: | ||
| align="center"| ● | | align="center"| ● | ||
| | | | ||
| − | |||
|- | |- | ||
! 5 | ! 5 | ||
| Строка 1431: | Строка 1337: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 6 | ! 6 | ||
| Строка 1440: | Строка 1345: | ||
| | | | ||
| | | | ||
| − | |||
|} | |} | ||
{| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | {| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | ||
| − | ! colspan="7"|B | + | ! colspan="7" style="background:#ffdead;"|B |
|- | |- | ||
! | ! | ||
| Строка 1454: | Строка 1358: | ||
|- | |- | ||
! 1 | ! 1 | ||
| + | | | ||
| align="center"| ● | | align="center"| ● | ||
| | | | ||
| Строка 1459: | Строка 1364: | ||
| | | | ||
| | | | ||
| − | |||
| − | |||
|- | |- | ||
! 2 | ! 2 | ||
| Строка 1469: | Строка 1372: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 3 | ! 3 | ||
| | | | ||
| | | | ||
| − | |||
| | | | ||
| | | | ||
| | | | ||
| − | + | | align="center"| ● | |
|- | |- | ||
! 4 | ! 4 | ||
| + | | | ||
| | | | ||
| | | | ||
| Строка 1486: | Строка 1388: | ||
| align="center"| ● | | align="center"| ● | ||
| | | | ||
| − | |||
| − | |||
|- | |- | ||
! 5 | ! 5 | ||
| Строка 1496: | Строка 1396: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 6 | ! 6 | ||
| Строка 1505: | Строка 1404: | ||
| | | | ||
| | | | ||
| − | |||
|} | |} | ||
{| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | {| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | ||
| − | ! colspan="7"|C | + | ! colspan="7" style="background:#ffdead;"|C |
|- | |- | ||
! | ! | ||
| Строка 1519: | Строка 1417: | ||
|- | |- | ||
! 1 | ! 1 | ||
| + | | align="center"| ● | ||
| | | | ||
| | | | ||
| Строка 1524: | Строка 1423: | ||
| | | | ||
| | | | ||
| − | |||
| − | |||
|- | |- | ||
! 2 | ! 2 | ||
| | | | ||
| − | |||
| | | | ||
| | | | ||
| | | | ||
| | | | ||
| − | + | | | |
|- | |- | ||
! 3 | ! 3 | ||
| | | | ||
| | | | ||
| + | | align="center"| ● | ||
| | | | ||
| | | | ||
| | | | ||
| − | |||
| − | |||
|- | |- | ||
! 4 | ! 4 | ||
| Строка 1549: | Строка 1444: | ||
| | | | ||
| | | | ||
| + | | align="center"| ● | ||
| | | | ||
| | | | ||
| − | |||
| − | |||
|- | |- | ||
! 5 | ! 5 | ||
| Строка 1559: | Строка 1453: | ||
| | | | ||
| | | | ||
| − | |||
| | | | ||
| − | + | | | |
|- | |- | ||
! 6 | ! 6 | ||
| Строка 1569: | Строка 1462: | ||
| | | | ||
| | | | ||
| − | | | + | | |
| − | |||
|} | |} | ||
{| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | {| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | ||
| − | ! colspan="7"|D | + | ! colspan="7" style="background:#ffdead;"|D |
|- | |- | ||
! | ! | ||
| Строка 1585: | Строка 1477: | ||
! 1 | ! 1 | ||
| | | | ||
| − | |||
| | | | ||
| | | | ||
| | | | ||
| | | | ||
| − | + | | | |
|- | |- | ||
! 2 | ! 2 | ||
| | | | ||
| + | | align="center"| ● | ||
| | | | ||
| | | | ||
| | | | ||
| | | | ||
| − | |||
| − | |||
|- | |- | ||
! 3 | ! 3 | ||
| Строка 1607: | Строка 1497: | ||
| | | | ||
| | | | ||
| − | | | + | | |
| − | |||
|- | |- | ||
! 4 | ! 4 | ||
| + | | | ||
| | | | ||
| | | | ||
| Строка 1616: | Строка 1506: | ||
| | | | ||
| align="center"| ● | | align="center"| ● | ||
| − | |||
| − | |||
|- | |- | ||
! 5 | ! 5 | ||
| Строка 1624: | Строка 1512: | ||
| | | | ||
| | | | ||
| + | | align="center"| ● | ||
| | | | ||
| − | |||
| − | |||
|- | |- | ||
! 6 | ! 6 | ||
| Строка 1634: | Строка 1521: | ||
| | | | ||
| | | | ||
| − | | | + | | align="center"| ● |
| − | |||
|} | |} | ||
| − | {| border="1" class="wikitable" style="width: 150px; height: 150px; " | + | {| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" |
| − | ! colspan="7"|E | + | ! colspan="7" style="background:#ffdead;"|E |
|- | |- | ||
! | ! | ||
| Строка 1655: | Строка 1541: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 2 | ! 2 | ||
| Строка 1664: | Строка 1549: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 3 | ! 3 | ||
| Строка 1673: | Строка 1557: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 4 | ! 4 | ||
| Строка 1682: | Строка 1565: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 5 | ! 5 | ||
| Строка 1691: | Строка 1573: | ||
| align="center"| ● | | align="center"| ● | ||
| | | | ||
| − | |||
|- | |- | ||
! 6 | ! 6 | ||
| Строка 1700: | Строка 1581: | ||
| | | | ||
| align="center"| ● | | align="center"| ● | ||
| − | |||
|} | |} | ||
| − | + | <div style="clear:both;"></div> | |
| − | |||
| − | |||
| + | Итерация <tex>m = 5</tex>. | ||
{| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | {| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | ||
| − | ! colspan="7"|A | + | ! colspan="7" style="background:#ffdead;"|A |
|- | |- | ||
! | ! | ||
| Строка 1724: | Строка 1603: | ||
| | | | ||
| | | | ||
| − | | | + | | align="center"| ● |
| − | |||
|- | |- | ||
! 2 | ! 2 | ||
| Строка 1734: | Строка 1612: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 3 | ! 3 | ||
| Строка 1743: | Строка 1620: | ||
| | | | ||
| align="center"| ● | | align="center"| ● | ||
| − | |||
|- | |- | ||
! 4 | ! 4 | ||
| Строка 1752: | Строка 1628: | ||
| align="center"| ● | | align="center"| ● | ||
| | | | ||
| − | |||
|- | |- | ||
! 5 | ! 5 | ||
| Строка 1761: | Строка 1636: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 6 | ! 6 | ||
| Строка 1770: | Строка 1644: | ||
| | | | ||
| | | | ||
| − | |||
|} | |} | ||
{| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | {| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | ||
| − | ! colspan="7"|B | + | ! colspan="7" style="background:#ffdead;"|B |
|- | |- | ||
! | ! | ||
| Строка 1784: | Строка 1657: | ||
|- | |- | ||
! 1 | ! 1 | ||
| + | | | ||
| align="center"| ● | | align="center"| ● | ||
| | | | ||
| | | | ||
| | | | ||
| − | | | + | | align="center"| ● |
| − | | | ||
| − | |||
|- | |- | ||
! 2 | ! 2 | ||
| Строка 1799: | Строка 1671: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 3 | ! 3 | ||
| | | | ||
| | | | ||
| − | |||
| | | | ||
| | | | ||
| | | | ||
| − | + | | align="center"| ● | |
|- | |- | ||
! 4 | ! 4 | ||
| + | | | ||
| | | | ||
| | | | ||
| Строка 1816: | Строка 1687: | ||
| align="center"| ● | | align="center"| ● | ||
| | | | ||
| − | |||
| − | |||
|- | |- | ||
! 5 | ! 5 | ||
| Строка 1826: | Строка 1695: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 6 | ! 6 | ||
| Строка 1835: | Строка 1703: | ||
| | | | ||
| | | | ||
| − | |||
|} | |} | ||
{| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | {| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | ||
| − | ! colspan="7"|C | + | ! colspan="7" style="background:#ffdead;"|C |
|- | |- | ||
! | ! | ||
| Строка 1849: | Строка 1716: | ||
|- | |- | ||
! 1 | ! 1 | ||
| + | | align="center"| ● | ||
| | | | ||
| | | | ||
| Строка 1854: | Строка 1722: | ||
| | | | ||
| | | | ||
| − | |||
| − | |||
|- | |- | ||
! 2 | ! 2 | ||
| | | | ||
| − | |||
| | | | ||
| | | | ||
| | | | ||
| | | | ||
| − | + | | | |
|- | |- | ||
! 3 | ! 3 | ||
| | | | ||
| | | | ||
| + | | align="center"| ● | ||
| | | | ||
| | | | ||
| | | | ||
| − | |||
| − | |||
|- | |- | ||
! 4 | ! 4 | ||
| Строка 1879: | Строка 1743: | ||
| | | | ||
| | | | ||
| + | | align="center"| ● | ||
| | | | ||
| | | | ||
| − | |||
| − | |||
|- | |- | ||
! 5 | ! 5 | ||
| Строка 1889: | Строка 1752: | ||
| | | | ||
| | | | ||
| − | |||
| | | | ||
| − | + | | | |
|- | |- | ||
! 6 | ! 6 | ||
| Строка 1899: | Строка 1761: | ||
| | | | ||
| | | | ||
| − | | | + | | |
| − | |||
|} | |} | ||
{| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | {| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" | ||
| − | ! colspan="7"|D | + | ! colspan="7" style="background:#ffdead;"|D |
|- | |- | ||
! | ! | ||
| Строка 1915: | Строка 1776: | ||
! 1 | ! 1 | ||
| | | | ||
| − | |||
| | | | ||
| | | | ||
| | | | ||
| | | | ||
| − | + | | | |
|- | |- | ||
! 2 | ! 2 | ||
| | | | ||
| + | | align="center"| ● | ||
| | | | ||
| | | | ||
| | | | ||
| | | | ||
| − | |||
| − | |||
|- | |- | ||
! 3 | ! 3 | ||
| Строка 1937: | Строка 1796: | ||
| | | | ||
| | | | ||
| − | | | + | | |
| − | |||
|- | |- | ||
! 4 | ! 4 | ||
| + | | | ||
| | | | ||
| | | | ||
| Строка 1946: | Строка 1805: | ||
| | | | ||
| align="center"| ● | | align="center"| ● | ||
| − | |||
| − | |||
|- | |- | ||
! 5 | ! 5 | ||
| Строка 1954: | Строка 1811: | ||
| | | | ||
| | | | ||
| + | | align="center"| ● | ||
| | | | ||
| − | |||
| − | |||
|- | |- | ||
! 6 | ! 6 | ||
| Строка 1964: | Строка 1820: | ||
| | | | ||
| | | | ||
| − | | | + | | align="center"| ● |
| − | |||
|} | |} | ||
| − | {| border="1" class="wikitable" style="width: 150px; height: 150px; " | + | {| border="1" class="wikitable" style="width: 150px; height: 150px; float: left;" |
| − | ! colspan="7"|E | + | ! colspan="7" style="background:#ffdead;"|E |
|- | |- | ||
! | ! | ||
| Строка 1985: | Строка 1840: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 2 | ! 2 | ||
| Строка 1994: | Строка 1848: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 3 | ! 3 | ||
| Строка 2003: | Строка 1856: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 4 | ! 4 | ||
| Строка 2012: | Строка 1864: | ||
| | | | ||
| | | | ||
| − | |||
|- | |- | ||
! 5 | ! 5 | ||
| Строка 2021: | Строка 1872: | ||
| align="center"| ● | | align="center"| ● | ||
| | | | ||
| − | |||
|- | |- | ||
! 6 | ! 6 | ||
| Строка 2030: | Строка 1880: | ||
| | | | ||
| align="center"| ● | | align="center"| ● | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|} | |} | ||
| − | + | <div style="clear:both;"></div> | |
== См. также == | == См. также == | ||
| Строка 2376: | Строка 1895: | ||
[[Категория: Теория формальных языков]] | [[Категория: Теория формальных языков]] | ||
[[Категория: Контекстно-свободные грамматики]] | [[Категория: Контекстно-свободные грамматики]] | ||
| + | [[Категория: Алгоритмы разбора]] | ||
Версия 22:51, 23 мая 2019
| Задача: |
| Пусть дана контекстно-свободная грамматика в нормальной форме Хомского и слово . Требуется выяснить, выводится ли это слово в данной грамматике. |
Содержание
Контекстно-свободная грамматика
| Определение: |
| Контекстно-свободная грамматика (КС-грамматика, бесконтекстная грамматика) — способ описания формального языка, представляющий собой четверку
, где:
|
Пример
Терминалы .
Нетерминалы .
Правила вывода :
Данная грамматика задает язык правильных скобочных последовательностей. Например, последовательность может быть выведена следующим образом:
Нормальная форма Хомского
Нормальная форма Хомского — нормальная форма КС-грамматик, в которой все продукции имеют вид:
- , где — нетерминал, а — терминал
- , где , , — нетерминалы, причем и не являются начальными нетерминалами
- , где — начальный нетерминал и — пустая строка (данная продукция необходима, если в языке присуствует пустая строка)
Можно показать, что любую КС-грамматику можно привести к нормальной форме Хомского.
Алгоритм
Алгоритм Кока-Янгера-Касами (англ. Cocke-Younger-Kasami algorithm, англ. CYK-алгоритм) — алгоритм, позволяющий по слову узнать, выводимо ли оно в заданной КС-грамматике в нормальной форме Хомского. Любую КС-грамматику можно привести к НФХ, поэтому алгоритм является универсальным для любой КС-грамматики.
Будем решать задачу динамическим программированием. Дана строка размером . Заведем для неё трехмерный массив размером , состоящий из логических значений, и тогда и только тогда, когда из нетерминала правилами грамматики можно вывести подстроку .
Рассмотрим все пары , где — константа и .
- . Инициализируем массив для всех нетерминалов, из которых выводится какой-либо символ строки . В таком случае , если в грамматике присутствует правило . Иначе .
- . Значения для всех нетерминалов и пар уже вычислены, поэтому . То есть, подстроку можно вывести из нетерминала , если существует продукция вида и такое , что подстрока выводима из , а подстрока выводится из .
После окончания работы значение содержит ответ на вопрос, выводима ли данная строка в данной грамматике, где — начальный символ грамматики.
Модификации
Количество способов вывести слово
Если массив будет хранить целые числа, а формулу заменить на , то — количество способов получить подстроку из нетерминала .
Минимальная стоимость вывода слова
Пусть — стоимость вывода по правилу . Тогда, если использовать формулу , то — минимальная стоимость вывода подстроки из нетерминала .
Таким образом, задача о выводе в КС-грамматике в нормальной форме Хомского является частным случаем задачи динамического программирования на подотрезке.
Асимптотика
Обработка правил вида выполняется за .
Проход по всем подстрокам выполняется за . В обработке одной подстроки присутствует цикл по всем правилам вывода и по всем разбиениям на две подстроки, следовательно обработка работает за . В итоге получаем конечную сложность .
Следовательно, общее время работы алгоритма — . Кроме того, алгоритму требуется память на массив объемом , где — количество нетерминалов грамматики.
Пример работы
Дана грамматика правильных скобочных последовательностей в нормальной форме Хомского.
Дано слово .
Инициализация массива .
| A | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ||||||
| 2 | ||||||
| 3 | ||||||
| 4 | ||||||
| 5 | ||||||
| 6 | ||||||
| B | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ||||||
| 2 | ||||||
| 3 | ||||||
| 4 | ||||||
| 5 | ||||||
| 6 | ||||||
| C | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ● | |||||
| 2 | ||||||
| 3 | ● | |||||
| 4 | ● | |||||
| 5 | ||||||
| 6 | ||||||
| D | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ||||||
| 2 | ● | |||||
| 3 | ||||||
| 4 | ||||||
| 5 | ● | |||||
| 6 | ● | |||||
| E | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ||||||
| 2 | ● | |||||
| 3 | ||||||
| 4 | ||||||
| 5 | ● | |||||
| 6 | ● | |||||
Заполнение массива .
Итерация .
| A | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ● | |||||
| 2 | ||||||
| 3 | ||||||
| 4 | ● | |||||
| 5 | ||||||
| 6 | ||||||
| B | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ● | |||||
| 2 | ||||||
| 3 | ||||||
| 4 | ● | |||||
| 5 | ||||||
| 6 | ||||||
| C | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ● | |||||
| 2 | ||||||
| 3 | ● | |||||
| 4 | ● | |||||
| 5 | ||||||
| 6 | ||||||
| D | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ||||||
| 2 | ● | |||||
| 3 | ||||||
| 4 | ||||||
| 5 | ● | |||||
| 6 | ● | |||||
| E | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ||||||
| 2 | ● | |||||
| 3 | ||||||
| 4 | ||||||
| 5 | ● | |||||
| 6 | ● | |||||
Итерация .
| A | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ● | |||||
| 2 | ||||||
| 3 | ||||||
| 4 | ● | |||||
| 5 | ||||||
| 6 | ||||||
| B | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ● | |||||
| 2 | ||||||
| 3 | ||||||
| 4 | ● | |||||
| 5 | ||||||
| 6 | ||||||
| C | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ● | |||||
| 2 | ||||||
| 3 | ● | |||||
| 4 | ● | |||||
| 5 | ||||||
| 6 | ||||||
| D | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ||||||
| 2 | ● | |||||
| 3 | ||||||
| 4 | ● | |||||
| 5 | ● | |||||
| 6 | ● | |||||
| E | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ||||||
| 2 | ● | |||||
| 3 | ||||||
| 4 | ||||||
| 5 | ● | |||||
| 6 | ● | |||||
Итерация .
| A | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ● | |||||
| 2 | ||||||
| 3 | ● | |||||
| 4 | ● | |||||
| 5 | ||||||
| 6 | ||||||
| B | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ● | |||||
| 2 | ||||||
| 3 | ● | |||||
| 4 | ● | |||||
| 5 | ||||||
| 6 | ||||||
| C | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ● | |||||
| 2 | ||||||
| 3 | ● | |||||
| 4 | ● | |||||
| 5 | ||||||
| 6 | ||||||
| D | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ||||||
| 2 | ● | |||||
| 3 | ||||||
| 4 | ● | |||||
| 5 | ● | |||||
| 6 | ● | |||||
| E | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ||||||
| 2 | ● | |||||
| 3 | ||||||
| 4 | ||||||
| 5 | ● | |||||
| 6 | ● | |||||
Итерация .
| A | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ● | |||||
| 2 | ||||||
| 3 | ● | |||||
| 4 | ● | |||||
| 5 | ||||||
| 6 | ||||||
| B | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ● | |||||
| 2 | ||||||
| 3 | ● | |||||
| 4 | ● | |||||
| 5 | ||||||
| 6 | ||||||
| C | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ● | |||||
| 2 | ||||||
| 3 | ● | |||||
| 4 | ● | |||||
| 5 | ||||||
| 6 | ||||||
| D | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ||||||
| 2 | ● | |||||
| 3 | ||||||
| 4 | ● | |||||
| 5 | ● | |||||
| 6 | ● | |||||
| E | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ||||||
| 2 | ● | |||||
| 3 | ||||||
| 4 | ||||||
| 5 | ● | |||||
| 6 | ● | |||||
Итерация .
| A | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ● | ● | ||||
| 2 | ||||||
| 3 | ● | |||||
| 4 | ● | |||||
| 5 | ||||||
| 6 | ||||||
| B | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ● | ● | ||||
| 2 | ||||||
| 3 | ● | |||||
| 4 | ● | |||||
| 5 | ||||||
| 6 | ||||||
| C | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ● | |||||
| 2 | ||||||
| 3 | ● | |||||
| 4 | ● | |||||
| 5 | ||||||
| 6 | ||||||
| D | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ||||||
| 2 | ● | |||||
| 3 | ||||||
| 4 | ● | |||||
| 5 | ● | |||||
| 6 | ● | |||||
| E | ||||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | ||||||
| 2 | ● | |||||
| 3 | ||||||
| 4 | ||||||
| 5 | ● | |||||
| 6 | ● | |||||