Барьерная синхронизация (3 алгоритма) — различия между версиями
Yeputons (обсуждение | вклад) |
Yeputons (обсуждение | вклад) (→Определение и полезность) |
||
| Строка 1: | Строка 1: | ||
== Определение и полезность == | == Определение и полезность == | ||
| + | |||
| + | Интервал <tex>[G, H]</tex> (<tex>G \subseteq H</tex>) называется барьерно синхронизирующим(?), если для любых событий <tex>e \in G</tex> и <tex>f \notin H</tex> верно, что $e \rightarrow f$. | ||
| + | |||
| + | Это сильнее [[Согласованный интервал|согласованных интервалов]]: те требуют лишь отсутствия стрелок справа налево (коих в барьере не может быть, потому что есть вообще все возможные стрелки слева направо, а в две стороны стрелки не бывает). | ||
| + | |||
| + | Как следствие, внутри любого барьерно-синхронизирующего интервала тоже есть согласованный срез (где-то, не знаем, где). | ||
| + | А искать такой интервал намного проще, чем [[Алгоритм Чанди-Лампорта|искать срез]] и по коду, и по количествуи сообщений (линия вместо квадрата). | ||
== Алгоритмы == | == Алгоритмы == | ||
Версия 19:19, 11 февраля 2019
Определение и полезность
Интервал () называется барьерно синхронизирующим(?), если для любых событий и верно, что $e \rightarrow f$.
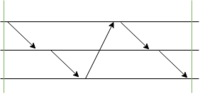
Это сильнее согласованных интервалов: те требуют лишь отсутствия стрелок справа налево (коих в барьере не может быть, потому что есть вообще все возможные стрелки слева направо, а в две стороны стрелки не бывает).
Как следствие, внутри любого барьерно-синхронизирующего интервала тоже есть согласованный срез (где-то, не знаем, где). А искать такой интервал намного проще, чем искать срез и по коду, и по количествуи сообщений (линия вместо квадрата).
Алгоритмы
- Централизованный: все посылают токен координатору, затем он посылает всем. сообщений, низкая задержка;
- Каждый посылает каждому токен. сообщений, низкая задержка;
- Token по кольцу, сообщений, высокая задержка.