Бустинг, AdaBoost
Содержание
Описание
Бустинг (англ. boosting) — мета-алгоритм машинного обучения. Основной идеей бустинга является комбинирование слабых функций, которые строятся в ходе итеративного процесса, где на каждом шаге новая модель обучается с использованием данных об ошибках предыдущих. Сильный обучающий алгоритм является классификатором, хорошо коррелирующим с верной классификацией, в отличие от слабого. Наравне с бустингом в мета-обучении также рассматривают такие понятия, как бэггинг (англ. bagging) и стэкинг[1] (англ. stacking). Бэггинг, в отличии от бустинга, использует параллельное обучение базовых классификаторов. Стэкинг же комбинирует результаты различных алгоритмов, получая тем самым более точный ответ.
Одним из недостатков бустинга является то, что он может приводить к построению громоздких композиций, состоящих из сотен алгоритмов. Такие композиции исключают возможность содержательной интерпретации, требуют больших объёмов памяти для хранения базовых алгоритмов и существенных затрат времени на вычисление классификаций.
Алгоритмы бустинга
| Определение: |
| Композицией $T$ алгоритмов называется суперпозиция алгоритмических операторов , корректирующей операции и решающего правила , где — пространство оценок, , Алгоритмы $a_t$ называют базовыми алгоритмами. |
Бустинг представляет собой композицию алгоритмов, в которых ошибки отдельных алгоритмов взаимно компенсируются. Например, в задаче классификации на два класса $Y = {-1, +1}$ в качестве пространства оценок принимают $R = \mathbb{R}$ и . Тогда базовые алгоритмы возвращают ответы $−1, 0, +1$. Ответ $b_t(x) = 0$ означает, что базовый алгоритм $b_t$ отказывается от классификации объекта $x$, и ответ $b_t(x)$ не учитывается в композиции. Получаем искомую композицию:
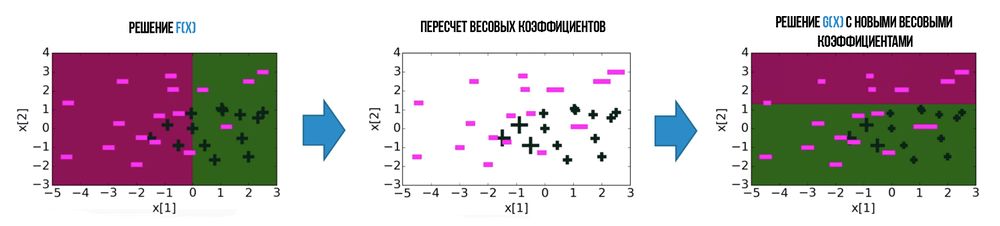
Большая часть алгоритмов бустинга основывается на итеративном обучении слабых классификаторов с дальнейшей сборкой их в сильный классификатор. Когда они добавляются, им обычно приписываются веса, обычно связанные с точностью обучения. После добавления слабого классификатора, веса пересчитываются («пересчёт весовых коэффициентов»). Неверно классифицированные входные данные получают больший вес, а правильно классифицированные экземпляры теряют вес. Таким образом, дальнейшее слабое обучение фокусируется на примерах, где предыдущие слабые обучения дали ошибочную классификацию.
Основное расхождение между многими алгоритмами бустинга заключается в методах определения весовых коэффициентов точек тренировочных данных и гипотез. Первым алгоритмом, который смог адаптироваться к слабому обучению был AdaBoost[2] (сокр. Adaptive Boosting), предложенный Шапире и Фройндом.
Алгоритмы бустинга могут использовать выпуклую или невыпуклую функцию потерь. Алгоритмы с выпуклой функцией, такие как AdaBoost и LogitBoost[3], могут некорректно классифицировать из-за случайного шума, так как не могут обучить базовым и поддающимся научению комбинациям слабых гипотез. Алгоритмы бустинга, основанные на невыпуклой функции потерь, такие как BrownBoost[4], позволяют избежать переобучения на данных с большим количеством "шума", откидывая зашумленные элементы.
Прикладное использование алгоритмов бустинга
Задача классификации объектов
Если даны изображения, содержащие различные известные в мире объекты, классификатор может быть обучен на основе них для автоматической классификации объектов в будущих неизвестных изображениях. Простые классификаторы, построенные на основе некоторых признаков изображения объекта, обычно оказываются малоэффективными в классификации. Использование методов бустинга для классификации объектов — путь объединения слабых классификаторов специальным образом для улучшения общей возможности классификации.
Классификация признаков является типичной задачей компьютерного зрения, где определяется, содержит ли изображение некоторую категорию объектов или нет. Идея тесно связана с распознаванием, идентификацией и обнаружением. Классификация по обнаружению объекта обычно содержит выделение признаков, обучение классификатора и применение классификатора к новым данным. Есть много способов представления категории объектов, например по анализу формы, с помощью модели «мешок слов», с помощью локальных описателей, таких как SIFT[5], и так далее. Примерами классификаторов с учителем служат наивные байесовские классификаторы[на 28.01.19 не создан], методы опорных векторов[на 28.01.19 не создан], смесь гауссиан и нейронные сети. Однако исследования показали, что категории объектов и их положение в изображениях могут быть обнаружены также с помощью обучения без учителя.
Задача ранжирования выдачи поисковых систем
Благодаря AdaBoost в мире появился градиентный бустинг (англ. gradient boosting) или GBM. Задачу ранжирования выдачи поисковых запросов рассмотрели с точки зрения функции потерь, которая штрафует за ошибки в порядке выдачи, поэтому было удобно внедрить GBM в ранжирование.
AdaBoost
Описание
Алгоритм может использоваться в сочетании с несколькими алгоритмами классификации для улучшения их эффективности. Алгоритм усиливает классификаторы, объединяя их в «комитет». AdaBoost является адаптивным в том смысле, что каждый следующий комитет классификаторов строится по объектам, неверно классифицированным предыдущими комитетами. AdaBoost чувствителен к шуму в данных и выбросам. Однако он менее подвержен переобучению по сравнению с другими алгоритмами машинного обучения.
AdaBoost вызывает слабые классификаторы в цикле . После каждого вызова обновляется распределение весов , которые отвечают важности каждого из объектов обучающего множества для классификации. На каждой итерации веса каждого неверно классифицированного объекта возрастают, таким образом новый комитет классификаторов «фокусирует своё внимание» на этих объектах.
Описание алгоритма
// function AdaBoost($X$, $Y$, $m$): //Инициализируем for i = 1..m do: end for for t = 1..T do: //$\epsilon$ — Взвешенная ошибка классификации, классификатор for i = 1..m do: // — нормализующий параметр, выбранный так, чтобы являлось распределением вероятностей, то есть , для end for end for //$H(x)$ — результирующий классификатор return $H$
Выражение для обновления распределения должно быть сконструировано таким образом, чтобы выполнялось условие:
Таким образом, после выбора оптимального классификатора для распределения , объекты , которые классификатор идентифицирует корректно, имеют веса меньшие, чем те, которые идентифицируются некорректно. Следовательно, когда алгоритм тестирует классификаторы на распределении , он будет выбирать классификатор, который лучше идентифицирует объекты неверно распознаваемые предыдущим классификатором.
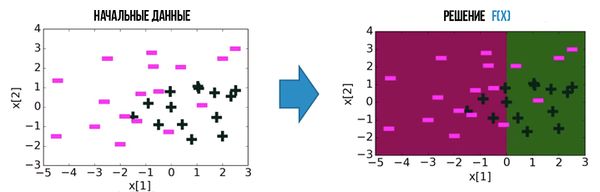
Пример работы
Рассмотрим набор данных, которые пометим как $-$ и $+$.
Для всех ошибочно классифицированных объектов увеличим веса, а для верно классифицированных уменьшим
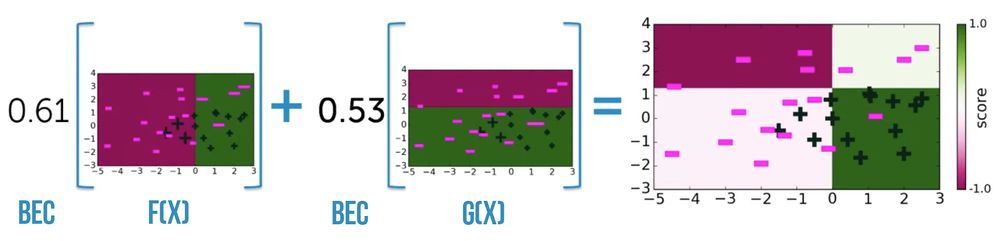
Рассмотрим результат после $2$-х итераций:
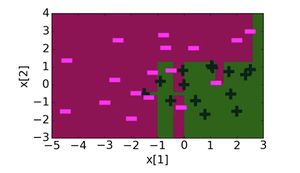
Как видно из последнего изображения, все, что находиться в "цветной" зоне, мы можем однозначно классифицировать, но тогда у нас появляются ошибки и "белые" зоны, которые мы не можем однозначно классифицировать. Рассмотрим алгоритм после $30$-ти итераций:
Теперь у нас все объекты классифицируются верно и число ошибок на выборке равно нулю.
Достоинства и недостатки
Достоинства:
- Простота реализации;
- Хорошая обобщающая способность. В реальных задачах удаётся строить композиции, превосходящие по качеству базовые алгоритмы. Обобщающая способность может улучшаться по мере увеличения числа базовых алгоритмов;
- Время построения композиции практически полностью определяется временем обучения базовых алгоритмов;
- Возможность идентифицировать выбросы. Это наиболее «трудные» объекты $x_i$, для которых в процессе наращивания композиции веса $w_i$ принимают наибольшие значения.
Недостатки:
- Склонен к переобучению при наличии значительного уровня шума в данных;
- Требует достаточно длинных обучающих выборок. Другие методы линейной коррекции, в частности, бэггинг, способны строить алгоритмы сопоставимого качества по меньшим выборкам данных.
Пример кода на python для scikit-learn
Классификатор sklearn.ensemble.AdaBoostClassifier[6] имеет 5 параметров: base_estimator, n_estimators, learning_rate, algorithm, random_state. Наиболее важными являются:
- base_estimator — базовый алгоритм. По умолчанию используется DecisionTreeClassifier(max_depth=1);
- n_estimators — максимальное количество оценок, после которого бустинг прекращается. Если произойдет полное совпадение, то закончится раньше;
- learning_rate — вклад каждой модели в весовые коэффициенты и значение по умолчанию равно $1$. Снижение этого параметра будет означать, что весовые коэффициенты буду увеличиваться или уменьшаться в небольшой степени, вынуждая модель дольше обучаться (но иногда повышается производительность).
from sklearn.ensemble import AdaBoostClassifier from sklearn import datasets from sklearn.model_selection import train_test_split from sklearn import metrics iris = datasets.load_iris() X = iris.data y = iris.target X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
abc = AdaBoostClassifier(n_estimators=50, learning_rate=1)
model = abc.fit(X_train, y_train)
y_pred = model.predict(X_test)
print("Accuracy:",metrics.accuracy_score(y_test, y_pred))
Accuracy: 0.8888888888888888
Теперь рассмотрим алгоритм с SVC в качестве базы:
from sklearn.svm import SVC
svc=SVC(probability=True, kernel='linear')
abc = AdaBoostClassifier(base_estimator=svc, n_estimators=50, learning_rate=1)
model = abc.fit(X_train, y_train)
y_pred = model.predict(X_test)
print("Accuracy:",metrics.accuracy_score(y_test, y_pred))
Accuracy: 0.9555555555555556
Пример на языке Scala
SBT зависимость:
libraryDependencies += "com.github.haifengl" %% "smile-scala" % "1.5.2"
Пример классификации датасета и вычисления F1 меры[7] используя smile.classification.adaboost[8]:
import smile.classification._ import smile.data._ import smile.plot._ import smile.read import smile.validation.FMeasure
val iris: AttributeDataset = read.table("iris.csv", delimiter = ",", response = Some((new NumericAttribute("class"), 2)))
val x: Array[Array[Double]] = iris.x()
val y: Array[Int] = iris.y().map(_.toInt)
val ada: AdaBoost = adaboost(x, y, ntrees = 500, maxNodes = 2)
val predictions: Array[Int] = x.map(ada.predict)
val f1Score = new FMeasure().measure(predictions, y)
plot(x, y, ada)
См. также
- Метод опорных векторов[на 28.01.19 не создан]
- Байесовская классификация[на 28.01.19 не создан]
- Мета-обучение
- Нейронные сети
- Оценка качества в задаче кластеризации
- CatBoost
Примечания
Источники информации
- AdaBoost — статья на machinelearning.ru
- AdaBoost — презентация по AdaBoost
- Example of AdaBoost in action — презентация на coursera.org
- Курс лекций по машинному обучению — Воронцов К.В.