Взвешенное дерево — различия между версиями
Algo1s097 (обсуждение | вклад) |
Shersh (обсуждение | вклад) м (переименовал Scapegoat tree в Взвешенное дерево: импортозамещение) |
(нет различий)
| |
Версия 19:35, 17 декабря 2016
Scapegoat-дерево — сбалансированное двоичное дерево поиска, обеспечивающее наихудшее время поиска, и — амортизирующее время вставки и удаления элемента. В отличие от большинства других самобалансирующихся бинарных деревьев поиска , которые обеспечивают худшем случае время поиска, Scapegoat деревья не требуют дополнительной памяти в узлах по сравнению с обычным двоичным деревом поиска: узел хранит только ключ и два указателя на своих потомков.
Содержание
Операции
| Определение: |
| Бинарное дерево поиска называется сбалансированным, если половина вершин расположены слева от корня, а другая половина справа. |
Введем обозначения: Квадратные скобки в обозначениях означают, что хранится это значение явно, а значит можно взять за время . Круглые скобки означают, что значение будет вычисляться по ходу дела то есть память не расходуется, но зато нужно время на вычисление.
— обозначение дерева, — корень дерева , — левый сын вершины , — правый сын вершины , — брат вершины (вершина, которая имеет с общего родителя), — глубина вершины . Это расстояние от неё до корня (количество ребер), — глубина дерева . Это глубина самой глубокой вершины дерева , — вес вершины . Это количество всех её дочерних вершин + 1 (она сама), — размер дерева . Это количество вершин в нём (вес корня), — максимальный размер дерева. Это максимальное значение, которое параметр принимал с момента последней перебалансировки.
Если перебалансировка произошла только что, то
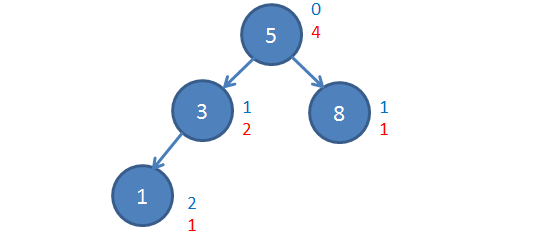
Синим цветом обозначены глубины вершин, а красным - их веса. Считается вес вершины следующим образом: для новой вершины вес = 1. Для её родителя вес = 1 (вес новой вершины) + 1 (вес самого родителя) + . Возникает вопрос — как посчитать ? Делается это рекурсивно. Это займёт время . Понимая, что в худшем случае придётся посчитать вес половины дерева — здесь появляется та самая сложность в худшем случае, о которой говорилось в начале. Но поскольку совершается обход поддерева -сбалансированного по весу дерева можно показать, что амортизированная сложность операции не превысит . В данном Scapegoat-дереве ,
Коэффициeнт — это число в диапазоне от , определяющее требуемую степень качества балансировки дерева.
| Определение: |
| Некоторая вершина называется α - сбалансированной по весу, если и . |
Перед тем как приступить к работе с деревом, выбирается параметр в диапазоне . Также нужно завести две переменные для хранения текущих значений и и обнулить их.
Поиск элемента
Пусть требуется найти в данном Scapegoat дереве какой-то элемент. Применим стандартный алгоритм для двоичного дерева поиска - идем от корня, если значение в вершине равно значению искомого элемента, возвращаем, если значение в вершине меньше, то рекурсивно запускаемся от левого поддерева, если больше, то, соответственно, от левого. Замечание: Дерево по ходу поиска искомой вершины не изменяется. Сложность операции поиска зависит от коэффициента и выражается формулой —
Таким образом, сложность получается логарифмическая, НО! При близком к мы получаем двоичный (или почти двоичный) логарифм, что означает практически идеальную скорость поиска. При близком к единице основание логарифма стремится к единице, а значит общая сложность стремится к .
Вставка элемента
Классический алгоритм вставки нового элемента: поиском ищем место, куда бы подвесить новую вершину, ну и подвешиваем. Легко понять, что это действие могло нарушить -балансировку по весу для одной или более вершин дерева. И вот теперь начинается то, что и дало название нашей структуре данных: требуется найти Scapegoat-вершину — вершину, для которой потерян -баланс и её поддерево должно быть перестроено. Сама только что вставленная вершина, хотя и виновата в потере баланса, Scapegoat-вершиной стать не может — у неё ещё нет потомков, а значит её баланс идеален. Соответственно, нужно пройти по дереву от этой вершины к корню, пересчитывая веса для каждой вершины по пути. Может возникнуть вопрос - нужно ли хранить ссылки на родителей? Поскольку к месту вставки новой вершины пришли из корня дерева — есть стек, в котором находится весь путь от корня к новой вершине. Берутся родителей из него. Если на этом пути от нашей вершины к корню встретится вершина, для которой критерий -сбалансированности по весу нарушился — тогда полностью перестраивается соответствующее ей поддерево так, чтобы восстановить -сбалансированность по весу. Сразу появляется вопрос — как делать перебалансировку найденной Scapegoat-вершины? Есть 2 способа перебалансировки, — тривиальный и чуть более сложный.
Тривиальный способ перебалансировки
- совершается обход всего поддерева Scapegoat-вершины (включая её саму) с помощью in-order обхода — на выходе получается отсортированный список (свойство In-order обхода бинарного дерева поиска).
- Находится медиана на этом отрезке и подвешивается в качестве корня поддерева.
- Для «левого» и «правого» поддерева рекурсивно повторяется та же операция.
Данный способ требует времени и столько же памяти.
Более сложный способ перебалансировки
Время работы перебалансировки вряд ли улучшится — всё-таки каждую вершину нужно «подвесить» в новое место. Но можно попробовать сэкономить память. Давайте посмотрим на 1 способ алгоритма внимательнее. Вот выбирается медиану, подвешивается в корень, дерево делится на два поддерева — и делится весьма однозначно. Никак нельзя выбрать «какую-то другую медиану» или подвесить «правое» поддерево вместо левого. Та же самая однозначность преследует и на каждом из следующих шагов. Т.е. для некоторого списка вершин, отсортированных в возрастающем порядке, будет ровно одно порождённое данным алгоритмом дерево. А откуда же берется отсортированный список вершин? Из in-order обхода изначального дерева. То есть каждой вершине, найденной по ходу in-order обхода перебалансируемого дерева соответствует одна конкретная позиция в новом дереве. И можно эту позицию рассчитать и без создания самого отсортированного списка. А рассчитав — сразу её туда записать. Возникает только одна проблема — этим затирается какая-то (возможно ещё не просмотренная) вершина — что же делать? Хранить её. Где? Ответ прост: выделять для списка таких вершин память. Но этой памяти нужно будет уже не , а всего лишь .
Представьте себе в уме дерево, состоящее из трёх вершин — корня и двух подвешенных как «левые» сыновья вершин. In-order обход вернёт нам эти вершины в порядке от самой «глубокой» до корня, но хранить в отдельной памяти по ходу этого обхода нам придётся всего одну вершину (самую глубокую), поскольку когда мы придём во вторую вершину, мы уже будем знать, что это медиана и она будет корнем, а остальные две вершины — её детьми. Т.е. расход памяти здесь — на хранение одной вершины, что согласуется с верхней оценкой для дерева из трёх вершин — . Таким образом, если нужно сэкономить память, то 2 способ перебалансировки дерева — лучший вариант.
Удаление элемента
Удаляется элемент из дерева обычным удалением вершины бинарного дерева поиска (поиск элемента, удаление, возможное переподвешивание детей). Далее следует проверка выполнения условия:
- ;
Если оно выполняется — дерево могло потерять - балансировку по весу, а значит нужно выполнить полную перебалансировку дерева (начиная с корня) и присвоить:
- ;
Сравнение с другими деревьями
Достоинства Scapegoat дерева
- По сравнению с такими структурами, как Красно-черное дерево, АВЛ-дерево и Декартово дерево, нет необходимости хранить какие-либо дополнительные данные в вершинах(а значит появляется выигрыш по памяти).
- Отсутствие необходимости перебалансировать дерево при операции поиска (а значит гарантируется максимальное время поиска , в отличии от структуры данных Splay-дерево, где гарантируется только амортизированное )
- При построении дерева выбирается некоторый коэффициент , который позволяет улучшать дерево, делая операции поиска более быстрыми за счет замедления операций модификации или наоборот. Можно реализовать структуру данных, а дальше уже подбирать коэффициент по результатам тестов на реальных данных и специфики использования дерева.
Недостатки Scapegoat дерева
- В худшем случае операции модификации дерева могут занять времени (амортизированная сложность у них по-прежнему , но защиты от плохих случаев нет).
- Можно неправильно оценить частоту разных операций с деревом и ошибиться с выбором коэффициента — в результате часто используемые операции будут работать долго, а редко используемые — быстро, что не очень хорошо.